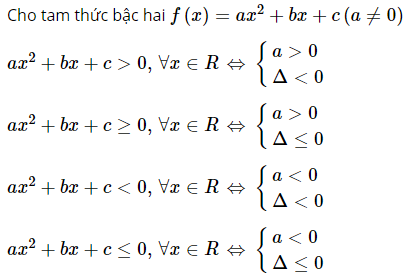TOPCLASS10 – GIẢI PHÁP HỌC TẬP TOÀN DIỆN DÀNH CHO 2K8
✅ Chuyển cấp nhẹ nhàng, chinh phục mọi bộ SGK - Bứt phá điểm 9,10
✅ Mô hình học tập 4 bước toàn diện: HỌC - LUYỆN - HỎI - KIỂM TRA
✅ Đội ngũ giáo viên luyện thi hàng đầu 16+ năm kinh nghiệm
✅ Dịch vụ hỗ trợ học tập đồng hành xuyên suốt quá trình học tập
1. Định lí đấu tam thức bậc hai
Định lý: Tam thức bậc hai đối với x là biểu thức có dạng: f(x) = ax2+bx+c, trong đó a, b, c là những hệ số (a ≠ 0).
Dấu của tam thức bậc hai
Với tam thức bậc hai: f(x) = ax2+bx+c (a ≠ 0), có Δ = b2+ ac:
+ Nếu Δ < 0 thì f(x) luôn cùng dấu với hệ số a với mọi x ∈ R
+ Nếu Δ = 0 thì f(x) có nghiệm kép x = -b/2a. Khi đó, f(x) có cùng dấu với hệ số a với mọi x ≠ -b/2a.
+ Nếu Δ > 0 thì f(x) có 2 nghiệm x1, x2 (x1 < x2), luôn cùng dấu với hệ số a với mọi x ∈(−∞;x1)∪(x2;+∞) và luôn trái dấu với hệ số a với mọi x ∈(x1, x2).
2. Bất phương trình bậc hai
Định nghĩa:
Bất phương trình bậc hai ẩn x là bất phương trình dạng ax2+bx+c < 0 (ax2+bx+c > 0; ax2+bx+c ≤ 0; ax2+bx+c ≥ 0) trong đó a, b, c là các số thực với a ≠ 0.
Giải bất phương trình bậc hai: Ta dùng định lí về dấu của tam thức bậc hai.
Chú ý: 
