TOPCLASS10 – GIẢI PHÁP HỌC TẬP TOÀN DIỆN DÀNH CHO 2K8
✅ Chuyển cấp nhẹ nhàng, chinh phục mọi bộ SGK - Bứt phá điểm 9,10
✅ Mô hình học tập 4 bước toàn diện: HỌC - LUYỆN - HỎI - KIỂM TRA
✅ Đội ngũ giáo viên luyện thi hàng đầu 16+ năm kinh nghiệm
✅ Dịch vụ hỗ trợ học tập đồng hành xuyên suốt quá trình học tập
Mục lục
1. Định nghĩa bất đẳng thức (BĐT)
2. Tính chất của BĐT
3. Phương pháp biến đổi tương đương của BĐT
4. BĐT chứa dấu giá trị tuyệt đối
5. BĐT Cauchy
1. Định nghĩa bất đẳng thức (BĐT)
Định nghĩa: Bất đẳng thức có dạng A>B,A<B,A≥B,A≤B, trong đó A là vế trái; B là vế phải (A, B là các biểu thức chứa số và các phép toán).
BĐT hệ quả: Từ BĐT A>B qua các phép biến đối ra được C>D, ta nói: BĐT C>D là BĐT hệ quả của BĐT A>B
BĐT tương đương: Từ BĐT A>B qua các phép biến đối ra được C>D và ngược lại, từ BĐT C>D ta biến đổi ngược lại ra BĐT A>B, ta nói rằng, 2 BĐT tương đương với nhau (kí hiệu: ).
2. Tính chất của BĐT
+ Tính chất bắc cầu:
+ Cộng 2 vế của BĐT với 1 số bất kì: A>B⇔A+C>B+C
+ Nhân 2 về của BĐT với 1 số khác: C>0 và A>B => AC>BC
C<0 và A>B =>AC<BC
+ Cộng hai BĐT cùng chiều: A>B và C>D ⇒ A+C>B+D
+ Nhân hai BĐT: A>B>0 và C>D>0 => AC>BD
+ Chuyển vế: A+B>C
+ Lũy thừa, khai căn: B>A≥0 (n ∈ N∗), ta có:
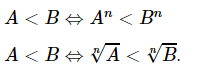
3. Phương pháp biến đổi tương đương của BĐT
Nội dung phương pháp: Sử dụng các phép biến đổi tương đương, để biến đổi BĐT ban đầu thành các BĐT tương đương với nói. Đến khi nào ta được BĐT cuối cùng là BĐT đúng.
Lưu ý: Nhớ các hằng đẳng thức đáng nhớ.
4. BĐT chứa dấu giá trị tuyệt đối
|a|−|b|≤|a+b|≤|a|+|b|
Lưu ý: Dấu chỉ xảy ra khi
|x|≤a ⇔ −a≤x≤a với
|x|≥a⇔ x≥a hoặc x≤−a với ∀a>0.
5. BĐT Cauchy
