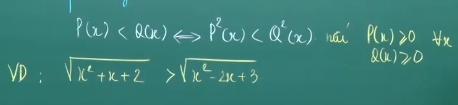TOPCLASS10 – GIẢI PHÁP HỌC TẬP TOÀN DIỆN DÀNH CHO 2K8

✅ Chuyển cấp nhẹ nhàng, chinh phục mọi bộ SGK - Bứt phá điểm 9,10

✅ Mô hình học tập 4 bước toàn diện: HỌC - LUYỆN - HỎI - KIỂM TRA

✅ Đội ngũ giáo viên luyện thi hàng đầu 16+ năm kinh nghiệm

✅ Dịch vụ hỗ trợ học tập đồng hành xuyên suốt quá trình học tập

1. Khái niệm bất phương trình (BPT) một ẩn

Khái niệm BPT một ẩn: BPT ẩn x là BPT có dạng f(x) < g(x) hoặc f(x) ≤ g(x)

f(x): Vế trái của BPT

g(x): Vế phải của BPT

Nghiệm của bất phương trình là giá tri của ẩn thay vào bất phương trình ta được một khẳng định đúng.

Lưu ý: Khí giải BPT là đi tìm tập nghiệm của BPT (không phải tìm 1 nghiệm)

BPT chứa tham số: Trong BPT vừa chứa ẩn x, vừa chứa một tham số nào đó (m,n…)

2. Hệ BPT một ẩn

+ Hệ BPT ẩn x gồm một số BPT ẩn x mà ta phải tìm các nghiệm chung

+ Mỗi giá trị x đồng thời là nghiệm của tất cả các BPT của hệ, được gọi là nghiệm của hệ BPT đã cho

+ Giải hệ BPT là tìm tập nghiệm của chúng: Giải tưng BPT 1 rồi lấy giao của các tập nghiệm.

3. Một số phép biến đổi BPT

BPT tương đương:

+ Hai BPT có cùng tập nghiệm (có thể là tập rỗng) là hai BPT tương đương.

+ Hai hệ BPT có cùng tập nghiệm là hai hệ BPT tương đương. (kí hiệu: “⇔”).

Phép biến đổi tương đương:

+ Để giải BPT (hệ BPT) ta biến đổi các BPT (hệ BPT) thành các BPT (hệ BPT) tương đương, cho đến khi được BPT (hệ BPT) đơn giản => Ta gọi là phép biến đổi đơn giản.

+ Phép cộng (trừ): P(x) < Q(x) ⇔ P(x) + f(x) < Q(x) + f(x)

P(x) < Q(x)+f(x) ⇔ P(x) – f(x) < Q(x)

+ Phép nhân (chia):

P(x) < Q(x) (1)

Nếu f(x) > 0 với ∀x => (1) ⇔ P(x)f(x) < Q(x)f(x)

Nếu  f(x) < 0 với ∀x => (1) ⇔ P(x)f(x) > Q(x)f(x)

+Bình phương: