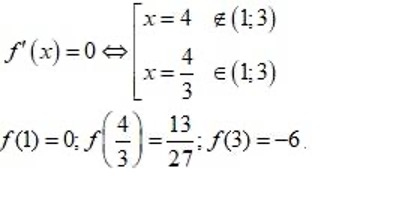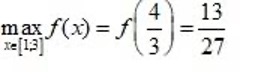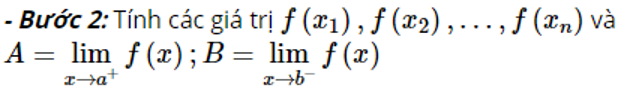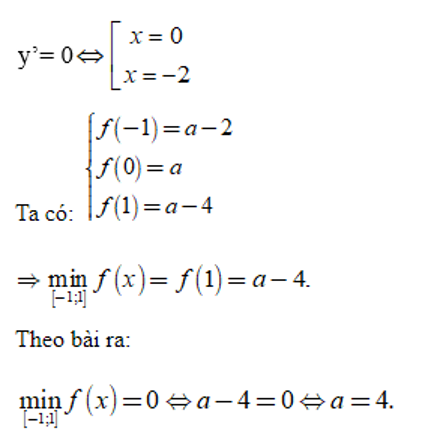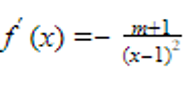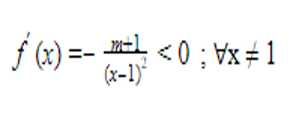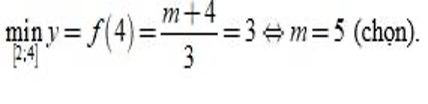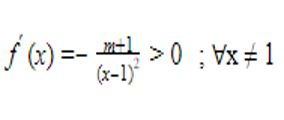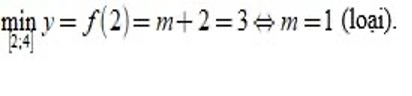Tổng hợp các dạng toán tìm giá trị lớn nhất nhỏ nhất của hàm số thường hay xuất hiện trong đề thi để các bạn tham khảo.

Tham khảo thêm:

• Đại số 12 (bài 3) Tìm giá trị lớn nhất nhỏ nhất của hàm số
• Giải bài tập toán lớp 12

Dạng 1: Tìm giá trị lớn nhất nhỏ nhất của hàm số trên đoạn

Cho hàm số y=f(x) xác định và liên tục trên đoạn [a;b]

Phương pháp làm bài:

– Bước 1: Tính y′ và giải phương trình y′=0 để tìm các nghiệm x1,x2,…xn  thỏa mãn điều kiện a≤x1<x2<…<xn≤b

– Bước 2: Tính các giá trị của f(a),f(x1),…,f(xn),f(b)

– Bước 3: So sánh các giá trị tính được ở phía trên và đưa ra kết luận:

• Giá trị lớn nhất tìm được trong số các giá trị ở trên là giá trị lớn nhất M của hàm số trên [a;b]
• Giá trị nhỏ nhất tìm được trong số các giá trị ở trên là giá trị nhỏ nhất m của hàm số trên [a;b]

Ví dụ 1: Tìm giá trị lớn nhất của hàm số f(x) = x³ – 8x² + 16x – 9 trên đoạn [1; 3] 

Nhận xét: Hàm số f(x) liên tục trên [1;3]

Ta có đạo hàm y’= 3x²– 16x + 16

Do đó ta có:

 

Ví dụ 2: Tìm giá trị nhỏ nhất của hàm số y = x(x + 2).(x + 4).(x + 6) + 5 trên nửa khoảng [-4; +∞)

* Ta có: y = (x2 + 6x).(x2 + 6x + 8) + 5.

Ta đặt t = x² + 6x. Khi đó ta được y = t.(t + 8) + 5 = t² + 8t + 5

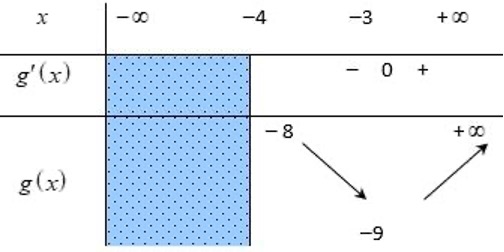
* Xét hàm số g(x)= x²  + 6x với x ≥ -4.

Ta có g'(x) = 2x + 6; g'(x) = 0 khi và chỉ khi x = -3

Lập bảng biến thiên:

Từ bảng biến thiên ta có t ∈ [-9; +∞)

* Yêu cầu của bài toán trở thành tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

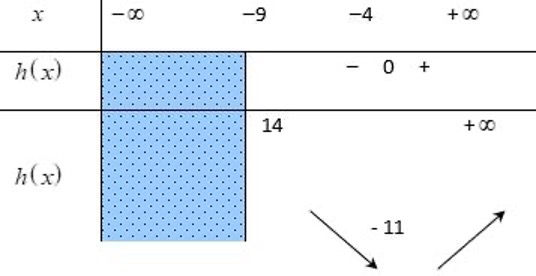
y = h(t)= t² + 8t + 5 với t ∈ [-9; +∞).

* Ta có h'(t) = 2t + 8

h'(t) = 0 khi t = – 4; 

Lập bảng biến thiên

Từ bảng biến thiên ta thấy:

Dạng 2: Tìm giá trị lớn nhất nhỏ nhất của hàm số trên khoảng

Cho hàm số y=f(x) xác định và liên tục trên (a;b)

Phương pháp làm bài:

– Bước 1: Tính f′(x) và giải phương trình y′=0 để tìm các nghiệm x1,x2,…xn thỏa mãn điều kiện a≤x1<x2<…<xn≤b

– Bước 3: So sánh các giá trị tính được ở trên và đưa ra kết luận.

• Nếu giá trị lớn nhất (hoặc giá trị nhỏ nhất) trong số các giá trị ở trên là A hoặc B thì kết luận hàm số không có giá trị lớn nhất (hoặc giá trị nhỏ nhất) trên khoảng (a;b)
• Nếu giá trị lớn nhất (hoặc giá trị nhỏ nhất) trong số các giá trị ở trên là f(xi), với i∈{1;2;…;n}thì kết luận hàm số đạt giá trị lớn nhất (hoặc giá trị nhỏ nhất) bằng f(xi) khi x=xi

Dạng 3: Tìm m để hàm số đạt giá trị lớn nhất nhỏ nhất thỏa mãn điều kiện cho trước

Cho hàm số f(x) xác định và liên tục trên đoạn [a;b]

Phương pháp làm bài: (chỉ áp dụng cho một số những bài toán dễ dàng tìm được nghiệm của y′)

– Bước 1: Tính y′ và giải phương trình y′=0 để tìm các nghiệm x1,x2,…xn

– Bước 2: Tính các giá trị của f(a),f(x1),…,f(xn),f(b)

– Bước 3: Biện luận theo tham số để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [a;b]

– Bước 4: Thay vào điều kiện của bài cho để tìm m

Ví dụ 1: Tìm m để giá trị lớn nhất của hàm số sau trên đoạn [0;1] bằng -4. Chọn đáp án đúng.

A. m = 1 hoặc m = -1      B. m = 2 hoặc m = -2

C. m = 3 hoặc m = -3      D. m = 4 hoặc m = -4

Đạo hàm:

Do đó hàm số f(x) đồng biến trên [0;1]

Nên ta có: 

Theo giả thiết ta có: 

⇔ m² = 9 nên m = 3 hoặc m = -3

→ ta chọn đáp án C.

Ví dụ 2: Tìm giá trị thực của tham số a để hàm số f(x) = -x3 – 3x2 + a có giá trị nhỏ nhất trên đoạn [-1; 1] là 0

1. a = 2      B. a = 6
2. a = 0      D. a = 4

Lời giải:

Đạo hàm f'(x) = -3x² – 6x

Xét phương trình:

→ ta chọn đáp án D.

Ví dụ 3: Cho hàm số sau: (với m là một tham số thực) thỏa mãn y =3

Mệnh đề nào dưới đây là đúng?

A. 3 < m < 4      B. 1 < m < 4

C. m > 4      D. m < -1

Lời giải: 

Đạo hàm: 

* Trường hợp 1.

Với m > -1 suy ra

 

nên hàm số f(x) nghịch biến trên mỗi khoảng xác định của nó.

Khi đó:

 

* Trường hợp 2.

Với m < -1 suy ra

do đó hàm số f(x) đồng biến trên mỗi khoảng xác định.

Khi đó ta được

Vậy m = 5 là giá trị cần tìm và thỏa mãn với điều kiện m > 4.

→ ta chọn đáp án C.