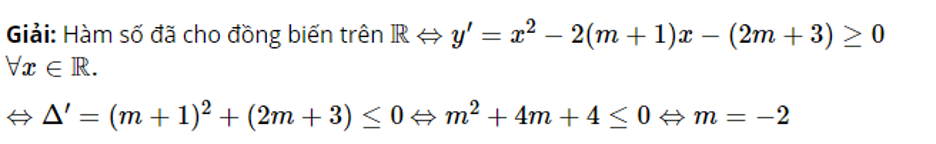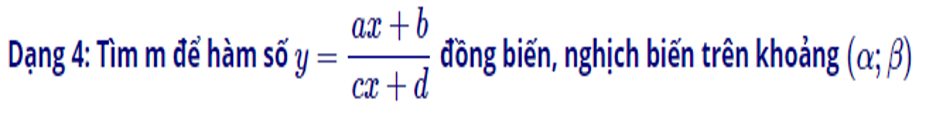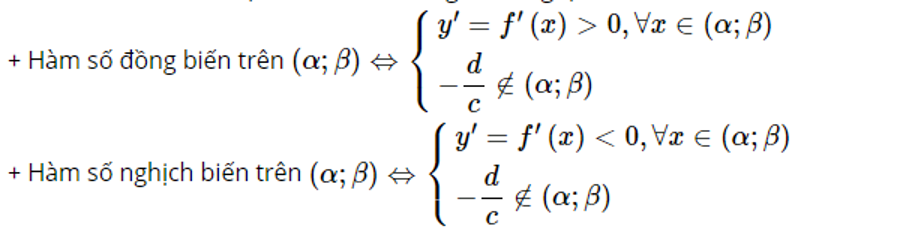Các dạng toán về sự đồng biến nghịch biến của hàm số thường gặp (Toán 12):

Tham khảo thêm:

• Sự đồng biến nghịch biến của hàm số
• Các dạng toán về cực trị hàm số đơn giản

Dạng 1: Tìm các khoảng đơn điệu của hàm số. 

Phương pháp làm bài:

– Bước 1: Tìm tập xác định của hàm số đã cho.

– Bước 2: Tính đạo hàm f′(x) , sau đó tìm các điểm x1,x2,…,xn  mà tại đó đạo hàm của hàm số bằng 0 hoặc không xác định.

– Bước 3: Xét dấu đạo hàm và đưa ra kết luận về khoảng đồng biến và nghịch biến của hàm số.

+ Các khoảng mà f′(x)>0 là các khoảng đồng biến của hàm số.

+ Các khoảng mà f′(x)<0 là các khoảng nghịch biến của hàm số.

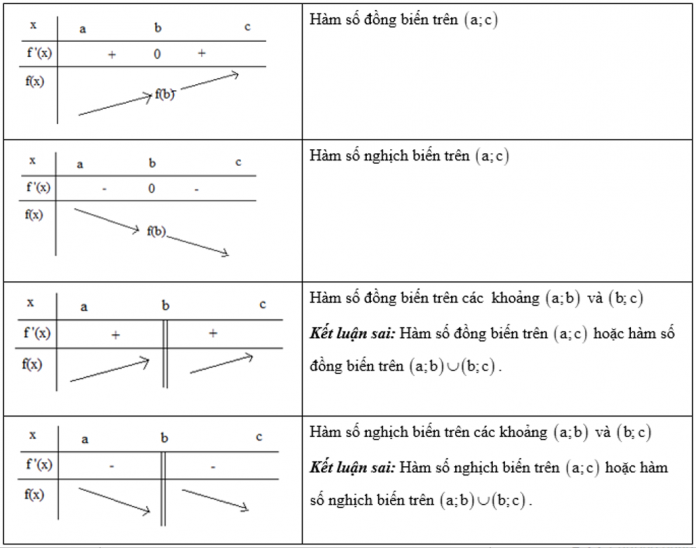
Một số trường hợp đặc biệt:

Dạng 2: Tìm giá trị của m để hàm số đơn điệu trên R.

Phương pháp làm bài:

– Bước 1: Tính f′(x).

– Bước 2: Nêu các điều kiện của bài toán:

+ Hàm số y=f(x) đồng biến trên R⇔y′=f′(x)⩾0,với ∀x∈R và y′=0 tại một hữu hạn điểm.

+ Hàm số y=f(x) nghịch biến trên R⇔y′=f′(x)⩽0,với ∀x∈R và y′=0 tại một hữu hạn điểm.

– Bước 3: Từ các điều kiện trên sử dụng các kiến thức về dấu của nhị thức bậc nhất và tam thức bậc hai để tìm m.

Dạng 3: Tìm m để hàm số đơn điệu trên miền D đã cho trước.

Phương pháp làm bài:

– Bước 1: Nêu các điều kiện để hàm số đơn điệu trên D:

+ Hàm số y=f(x) đồng biến trên D⇔y′=f′(x)⩾0, với ∀x∈D.

+ Hàm số y=f(x) nghịch biến trên D⇔y′=f′(x)⩽0,với ∀x∈D.

– Bước 2: Từ điều kiện trên hãy sử dụng các cách suy luận khác nhau cho từng bài toán để tìm m.

Bước 3: Kết luận

Ví dụ 3: Hàm số y = x³ + 3x² + mx + m đồng biến trên tập xác định chỉ khi giá trị của m là:

1. m ≤ 1
2. m ≥ 3
3. -1 ≤ m ≤ 3
4. m < 3

Lời giải

Tập xác định của hàm số :  D = R

Tính đạo hàm y’ = 3x² + 6x + m

Để hàm số đồng biến trên R ⇔ y’ ≥ 0 ⇔ 3x² + 6x + m ≥ 0 với mọi x ∈ R (*)

⇔ Δ’ ≤ 0 ⇔ 9 – 3m ≤ 0 ⇔ m ≥ 3

Chọn đáp án B.

Dạng 4: Tìm m để hàm số đồng biến, nghịch biến trên khoảng

– Bước 1: Tính y′

– Bước 2: Nêu điều kiện để hàm số đồng biến và nghịch biến:

– Bước 3: Đưa ra kết luận.

Nắm chắc kiến thức bài 1 Toán 12 thông qua Các dạng toán về sự đồng biến nghịch biến của hàm số