Sang hè, nghĩa là teen 2k2 sẽ đối mặt với chương trình Toán lớp 11, trong đó Toán lượng giác 11 được các anh chị 2k -2k1 đánh giá là một trong những phần kiến thức thú vị nhưng cũng vô cùng khó lấy điểm, vì thế nếu teen 2k2 muốn cán mốc điểm 8, 9 lượng giác thì hãy nhớ kỹ 2 tips sau.

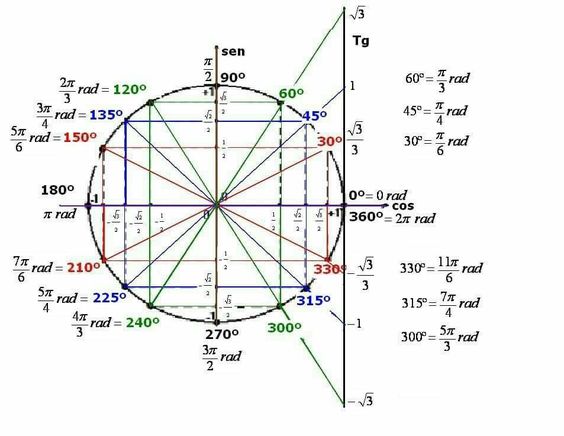
Trước hết, để giải 1 bài toán lượng giác, teen 2k2 cần phải tìm hiểu 1 bài toán tổng thể, tránh vội vàng đi ngay vào chi tiết. Tức là, teen 2k2 phải nắm rõ những yêu cầu của đề bài toán: Phương trình ở dạng cơ bản hay không mẫu mực, sau đó đưa về dạng tối ưu để tìm đáp án cuối cùng

Tiếp cận bài toán theo phương pháp tổng thể trước

Đầu tiên teen 2k2 cần nhận dạng phương trình lượng giác, sau khi nhận dạng được phương trình thì biến đổi phương trình đó về dạng quen thuộc và áp dụng các công thức cơ bản để giải toán. Cuối cùng teen kiểm tra các kết quả để đảm bảo phương trình không bỏ sót nghiệm, không thừa nghiệm, tránh các sai lầm phổ biến thường gặp.

TOPCLASS 2024 - CHƯƠNG TRÌNH HỌC TOÀN DIỆN

CHẮC KIẾN THỨC LỚP 11 - BẤT CHẤP CHƯƠNG TRÌNH HỌC KHÓ

• RÈN LUYỆN KỸ NĂNG TỰ HỌC - TƯ DUY GIẢI QUYẾT VẤN ĐỀ
• ĐA DẠNG HÌNH THỨC HỌC - PHÙ HỢP MỌI NHU CẦU
• TOP THẦY CÔ DANH TIẾNG ĐỒNG HÀNH PHÁT TRIỂN TOÀN DIỆN KIẾN THỨC & KỸ NĂNG
• DỊCH VỤ HỖ TRỢ ĐỒNG HÀNH TRONG SUỐT QUÁ TRÌNH HỌC TẬP

Ưu đãi đặt chỗ sớm - Giảm đến 45%! Áp dụng cho PHHS đăng ký trong tháng này!

HỌC THỬ MIỄN PHÍ ĐĂNG KÝ NGAY

Xử lý gọn bài toán bằng phương pháp chi tiết

Để xử lý gọn bài toán lượng giác một cách chi tiết teen phải thuộc lòng các công thức nghiệm và ghi nhớ các trường hợp nghiệm đặc biệt khi bằng 0; 1; -1  để làm cho nhanh. Bởi vì các phương trình khó cũng sẽ đưa về cơ bản để giải thôi nhé!

Khi đã nắm chắc phương trình cơ bản rồi, teen 2k2 sẽ bắt đầu tiếp cận giải các phương trình mẫu mực thường gặp, đó là:

asinx + b = 0; atanx + b = 0…; asin2(x) + bsinx + c = 0…

– Bậc nhất đối vói sinx, cosx:

asinx + bcosx = c

– Bậc hai đối với sinx, cosx:

asin(2)x + bsinxcosx + ccos(2)x = d

– Phương trình đối xứng đối với sinx và cosx:

a(sinx +/- cosx) + bsinxcosx = c

Ví dụ: cos6x+cos4x+cos2x+1=0  (1)

Ta đặt y=2x và c=cos(2x)=cos(y)

Phương trình ban đầu sẽ thành:

cos(3y)+cos(2y)+cosy+1=0  (2)

⇔ 4c3−3c+2c2−1+c+1=0 (3)

⇔4c3+2c2−2c=0

⇔2c(2c2+c−1)=0

⇔2c(c+1)(2c−1)=0

⇔c=0 hoặc c=−1 hoặc c=1/2

Vì vậy ta có:

cos(2x)=0 hoặc cos(2x)=−1 hoặc cos(2x)=½

2x=π/2+πk hoặc 2x=π+2πk hoặc 2x=π/3+2πk hoặc 2x=2π/3+2πk

Áp dụng điều kiện ta có  2x=π/2+2πk hoặc 2x=−π/2+2πk

Áp dụng điều kiện đầu bài, vậy kết quả của x là:

x={π/4,−π/4,π/2,π/6,π/3}+kπ

Ở ví dụ trên, phương trình (1) được nhìn nhận tổng thể, dùng phương pháp đặt ẩn quy đổi về dạng phương trình bậc 2 (phương trình (1) biến đổi sang phương trình (3)). Sau đó, teen có thể dễ dàng giải được phương trình bậc 2 cơ bản, giải ẩn và tìm được kết quả yêu cầu.

Ngoài ra, lượng giác còn dạng phương trình không mẫu mực, dạng này ở mức độ tương đối khó chỉ phù hợp với các teen học lực khá trở lên. Tuy nhiên các teen 2k2 với học lực trung bình vẫn có thể biến đổi dạng toán khó nhằn này về dạng quen thuộc nếu thực hiện đúng theo quy trình giải toán lượng giác từ tổng thể đến chi tiết nhé!!! Bật mí cho teen thêm bí quyết “xử đẹp” toán lượng giác ở đây:  http://bit.ly/2Kxcxqo