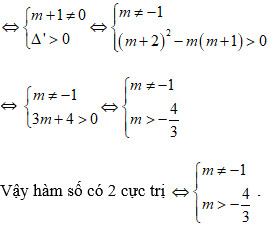Tìm m để hàm số có 2 cực trị | hàm bậc 3

0

Tìm m để hàm số có 2 trực trị (hàm bậc ba) cực hay, có lời giải chi tiết để các bạn tham khảo:

TOPUNI 2025 - GIẢI PHÁP LUYỆN THI ĐẠI HỌC TOÀN DIỆN
Đồng hành cùng 2K7 chắc vé Đại học TOP
  • Bất chấp biến động thi cử, lộ trình toàn diện cho mọi kỳ thi
  • Hệ thống trọn gói đầy đủ kiến thức theo sơ đồ tư duy, dễ dàng ôn luyện
  • Đội ngũ giáo viên luyện thi nổi tiếng với 17+ năm kinh nghiệm
  • Dịch vụ hỗ trợ học tập đồng hành xuyên suốt quá trình ôn luyện
Ưu đãi đặt chỗ sớm - Giảm đến 45%! Áp dụng cho PHHS đăng ký trong tháng này!

Tìm m để hàm số có 2 cực trị (Phương Pháp)

Xét hàm số sau đây y = ax3 + bx2 + cx + d với (a ≠ 0)

Khi đó ta có

  • y’ = 3ax2 + 2bx + c;
  • y’ = 0 ⇔ 3ax2 + 2bx + c = 0

Hàm số đã cho có 2 điểm cực trị ⇔ phương trình y’ = 0 có 2 nghiệm phân biệt

⇔ Δ’ > 0 ⇔ b2 – 3ac > 0

Dạng bài tìm m để hàm số có 2 cực trị có đáp án

Tìm m để hàm số có 2 cực trị (ví dụ số 1)

 Số giá trị nguyên của m ∈ [-10;10] để hàm số

có cực đại và cực tiểu là:

A. 20

B. 25

C. 13

D. 4

Lời giải chi tiết:

  • Đáp án đúng: A

Ta có y’ = x2 + 2mx – (1 – 2m) với y’ = 0 ⇔ x2 + 2mx – (1 – 2m) = 0

Hàm số đã cho có điểm cực đại và cực tiểu ⇔ phương trình y’ = 0 có 2 nghiệm phân biệt

⇔ Δ’ > 0 ⇔ m2 + (1 – 2m) > 0 ⇔ (m – 1)2 > 0 vậy m ≠ 1 thỏa mãn yêu cầu

Kết hợp với điều kiện m nguyên và m ∈ [-10;10] thì sẽ có 20 giá trị của m thỏa mãn.

Tìm m để hàm số có 2 cực trị (ví dụ số 2)

 Với giá trị nào của tham số m thì hàm số y = x3 – 3x2 + 3(1 – m2)x + 1 có hai điểm cực trị.

A. m ≠ 2

B. m ∈ R

C. m ≠ 0

D. Không tồn tại tham số m

Lời giải chi tiết

  • Đáp án đúng: C

Ta có y’ = 3x2-6x + 3(1 – m2) với y’ = 0 ⇔ x2-2x + 1 – m2 = 0

Hàm số đã cho có hai điểm cực trị ⇔ phương trình y’ = 0 cần có 2 nghiệm phân biệt

⇔ Δ’ > 0 ⇔ 1 – (1 – m2)>0 ⇔ m2>0 vậy m ≠ 0 thỏa mãn yêu cầu

Tìm m để hàm số có 2 cực trị (Ví dụ số 3) 

Cho hàm số có dạng y = -2x3 + (2m – 1)x2 – (m2 – 1)x – 2. Số giá trị nguyên của tham số m để hàm số đã cho có 2 điểm cực trị là:

A. 2

B. 5

C. 1

D. 9

Lời giải chi tiết:

  • Đáp án đúng: B

Chúng ta có y’ = -6x2 + 2(2m – 1)x – (m2 – 1)

Để hàm số đã cho có được 2 điểm cực trị ⇔ phương trình y’ = 0 có 2 nghiệm phân biệt

 

Do m là số nguyên nên m ∈ {-3;-2;-1;0;1}

Vậy sẽ có tất cả 5 giá trị nguyên của m thỏa mãn yêu cầu đề bài.

Tìm m để hàm số có 2 cực trị (ví dụ số 4) 

Tìm tất cả các giá trị của tham số  m để hàm số

 sẽ có 2 điểm cực trị.

Lời giải chi tiết:

Ta có y’ = (m + 1)x2 + 2(m + 2)x + m

Hàm số đã cho sẽ có 2 điểm cực trị ⇔ phương trình y’ = 0 có 2 nghiệm phân biệt

 

RELATED ARTICLESMORE FROM AUTHOR