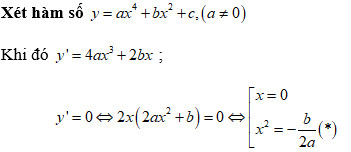Tìm m để hàm trùng phương có duy nhất 1 điểm cực trị cực hay, có lời giải để các bạn tham khảo (Toán lớp 12).

Tham khảo thêm:

• Cực trị của hàm số
• Cực trị hàm trị tuyệt đối
• Tìm m để hàm số có 2 cực trị

Cách tìm m để hàm số có đúng 1 cực trị

Khi đó hàm số sẽ có 1 điểm cực trị ⇔ phương trình (*) vô nghiệm hoặc phải có nghiệm kép bằng 0 ⇔ ab ≥ 0

Chú ý:

– Hàm trùng phương sẽ có đúng một cực trị và là cực tiểu khi:

– Hàm trùng phương sẽ có đúng một cực trị và là cực đại khi:

Tìm m để hàm số có đúng 1 cực trị có đáp án

*Ví dụ 1: Cho hàm số sau: $y=\left(\mathrm{1\; –}m\right){\mathrm{x^}}^4–m{\mathrm{x²}}^{}+2m–1$. Tìm  để hàm số đã cho có đúng 1 điểm cực trị.

*Ví dụ 2: Tìm tất cả các giá trị thực của tham số m để hàm số sau đây: y = -2x⁴ + (3m – 6)x² + 3m – 5 có duy nhất 1 điểm cực trị.

Lời giải chi tiết:

Hàm số y = -2x⁴ + (3m – 6)x² + 3m – 5 có 1 điểm cực trị ⇔ -2(3m – 6) ≥ 0 ⇔ (3m – 6) ≤ 0 ⇔ m ≤ 2

*Ví dụ 3: Với giá trị nào của tham số m thì hàm số y = (m – 1)x⁴ + 2x² + 3 sẽ có duy nhất 1 điểm cực trị

Lời giải chi tiết:

– Với m = 1 thì hàm số đã cho sẽ trở thành y = 2x² + 3, đây chính là hàm số bậc 2 nên sẽ có duy nhất 1 cực trị

→ Vậy m = 1 thỏa mãn

– Với m ≠ 1 thì hàm số đã cho sẽ có 1 điểm cực trị ⇔ (m – 1).2 ≥ 0 ⇔ m ≥ 1

→ Vậy hàm số sẽ có duy nhất nhất 1 điểm cực trị ⇔ m ≥ 1

*Ví dụ 4: Tìm tất cả các giá trị của m để hàm số sau đây: y = (m – 1)x⁴ + (m + 2)x² + 1 sẽ có duy nhất 1 điểm cực trị và đó chính là điểm cực đại.

Lời giải chi tiết

– Với m = 1 thì hàm số đã cho sẽ trở thành y = 3x² + 1 , đây chính là hàm số bậc 2 có hệ số a = 3 > 0 nên sẽ có duy nhất 1 điểm cực tiểu. Vậy loại m = 1

– Với m ≠ 1 thì hàm số đã cho sẽ có duy nhất 1 điểm cực trị và đó chính là điểm cực đại

Vậy hàm số đã cho sẽ có duy nhất 1 điểm cực trị và đó chính là điểm cực đại ⇔ m ≤ -2

Trên đây là hướng dẫn chi tiết cách Tìm m để hàm số có đúng 1 cực trị đối với Hàm trùng phương do butbi tổng hợp. Chúc các bạn học tốt.