Ở bài viết này, HOCMAI gửi tới các em học sinh khối 12 bài viết Đề cương ôn thi học kì 1 Toán 12 đầy đủ và chi tiết nhất. Tất cả những kiến thức Toán học  mà các em cần ngay lúc này đều được HOCMAI tổng hợp và biên soạn kỹ lưỡng trong bài viết. Các em hãy tham khảo bài viết này thật kĩ, ôn luyện kiến thức cũng như đề thi để chuẩn bị thật kỹ càng cho kỳ thi HK1 sắp tới nhé!

⇒ Các bài viết tham khảo thêm:

• Đề cương ôn thi học kì 1 Ngữ Văn 12
• Đề cương ôn thi học kì 1 Tiếng Anh 12
• Đề cương ôn thi học kì 1 môn Lý 12
• Đề cương ôn thi học kì 1 môn Hóa 12
• Đề cương ôn thi học kì 1 môn Sinh 12

A. KIẾN THỨC TRỌNG TÂM TOÁN ĐẠI SỐ

Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số

1. Đồ thị Hàm số

a) Hàm số bậc ba

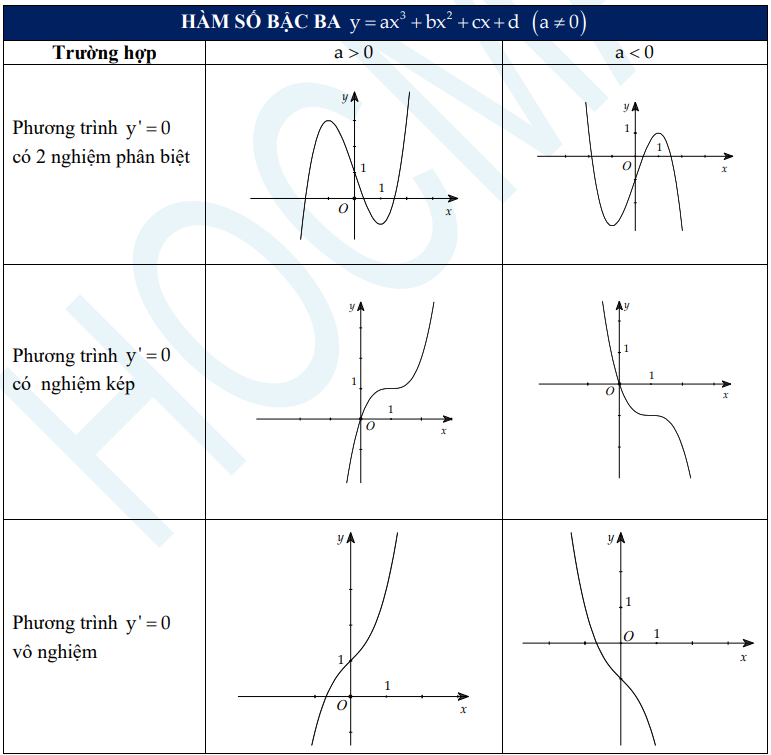
b) Hàm số bậc bốn trùng phương

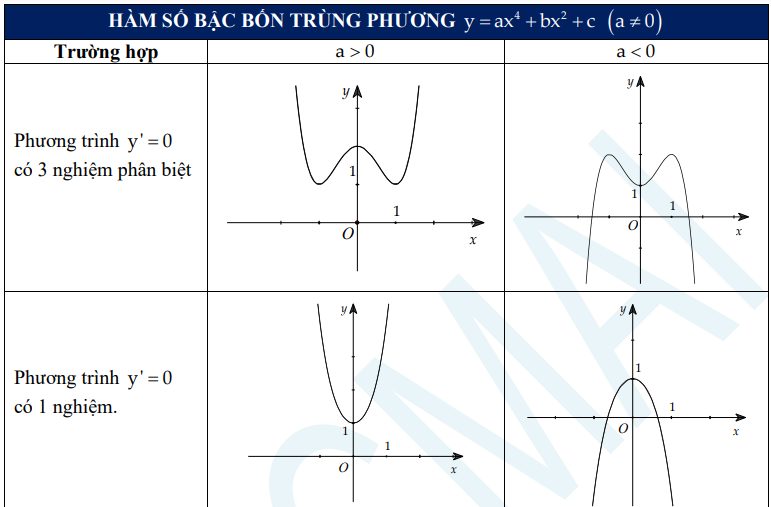
c) Hàm số y = (ax + b) / (cx + d) (c ≠ 0; ad – bc ≠ 0)

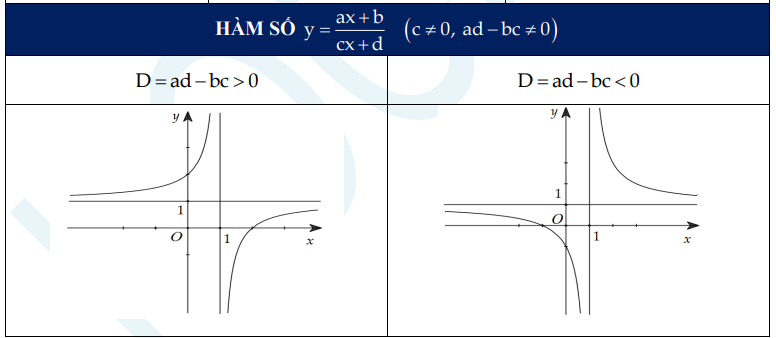
d) Hàm trị tuyệt đối

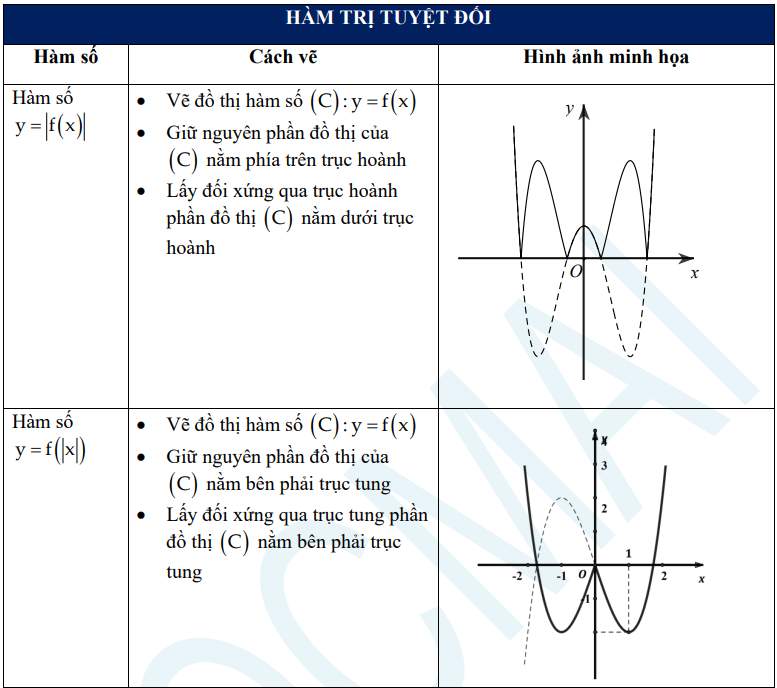
2. Sự đồng biến, nghịch biến của hàm số

Điều kiện để hàm số đồng biến, nghịch biến ở trên khoảng (a; b)

• Để hàm số đồng biến trên khoảng (a; b) thì f’(x) ≥ 0, với mọi x ∈ (a; b)
• Để hàm số nghịch biến trên khoảng (a; b) thì f’(x) ≤ 0, với mọi x ∈ (a; b) 

3. Quy tắc xét tính đơn điệu của hàm số

4. Quy tắc tìm cực trị của hàm số y = f(x)

Quy tắc 1:

Quy tắc 2:

5. Quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số liên tục trên một đoạn

6. Tiệm cận của đồ thị hàm số

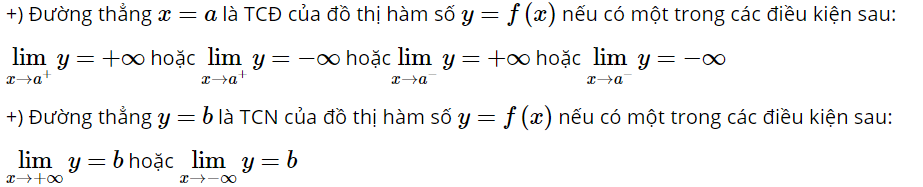
Các dạng bài tập thường gặp:

• Dạng 1: Tìm các khoảng đơn điệu của hàm số.
• Dạng 2: Tìm giá trị của m để hàm số đơn điệu trên R.
• Dạng 3: Tìm cực trị của hàm số.
• Dạng 4: Tìm điều kiện của tham số để hàm số có GTLN, GTNN thỏa mãn điều kiện cho trước.
• Dạng 5. Tìm tiệm cận đứng, tiệm cận ngang của đồ thị hàm số
• Dạng 6: Tìm điều kiện của tham số để đồ thị hàm số phân thức có tiệm cận đứng.
• Dạng 7. Sự tương giao của đồ thị hàm số
• Dạng 8: Viết phương trình tiếp tuyến của đồ thị

Chương 2: Hàm số lũy thừa, hàm số mũ và hàm số logarit

1. Lũy thừa và logarit

2. Hàm số mũ và hàm số logarit

3. Phương trình mũ, phương trình logarit

4. Bất phương trình mũ và logarit

5. Một vài lưu ý

Chương 3: Nguyên hàm. Tích phân và ứng dụng

1. Nguyên hàm

a) Bảng nguyên hàm của một số hàm cơ bản

2. Tích phân

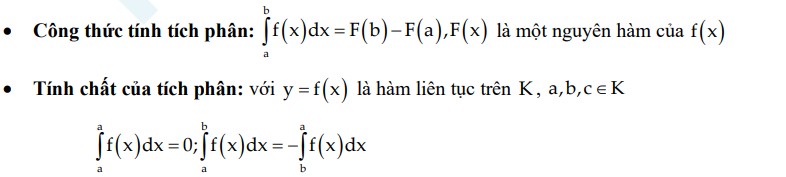
• Công thức tính diện tích và thể tích:

– Diện tích hình phẳng:

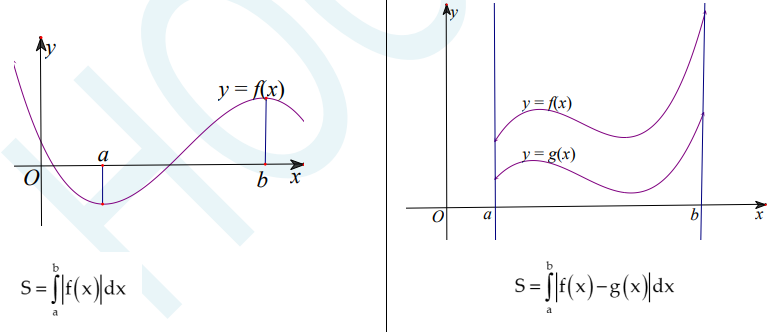
– Thể tích của vật thể:

Cắt vật thể V bởi hai mặt phẳng (P) và (Q) vuông góc cùng với trục Ox lần lượt tại

x = a, x = b (a<b). Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x(a ≤ x ≤ b) cắt V theo thiết diện có diện tích S(x). Giả sử S(x) liên tục trên [a; b]. Người ta chứng minh được rằng, thể tích V của phần vật thể V giới hạn bởi hai mặt phẳng (P) và (Q) được tính bởi công thức:

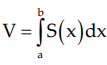
– Thể tích của khối tròn xoay:

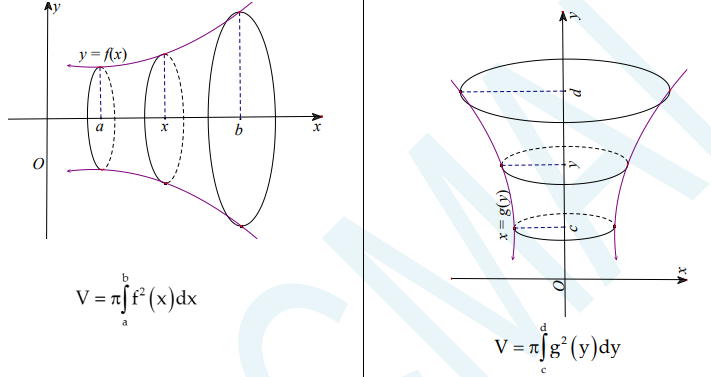
Các dạng bài tập thường gặp:

• Dạng 1: Xác định nguyên hàm, tích phân bằng định nghĩa, tính chất
• Dạng 2: Xác định nguyên hàm, tích phân bằng phương pháp đổi biến
• Dạng 3: Xác định nguyên hàm, tích phân bằng phương pháp từng phần
• Dạng 4: Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số y = f1(x); y = f2(x)
• Dạng 5: Tính thể tích vật thể
• Dạng 6: Tính thể tích khối tròn xoay sinh ra bởi hình phẳng giới hạn bởi đồ thị hai hàm số y = f1(x); y = f2(x)
• Dạng 7: Bài toán thực tế

B. KIẾN THỨC TRỌNG TÂM TOÁN HÌNH HỌC

Chương 1: Khối đa diện

1. Hình đa diện, khối đa diện

a) Khái niệm về hình đa diện

Hình đa diện (H) là hình được tạo bởi một số hữu hạn những đa giác thỏa mãn hai tính chất:

• Hai đa giác phân biệt chỉ có thể hoặc là không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ có 01 cạnh chung.
• Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng 02 đa giác. Mỗi đa giác như thế  được gọi là một mặt của hình đa diện (H). Các cạnh, đỉnh của các đa giác ấy theo thứ tự gọi là các cạnh, đỉnh của hình đa diện (H).

Khối đa diện là phần không gian được giới hạn bởi 01 hình đa diện (H), kể cả hình đa diện đó.

b) Khối đa diện lồi

Khối đa diện (H) được gọi là khối đa diện lồi nếu như đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó đa diện giới hạn (H) sẽ được gọi là đa diện lồi.

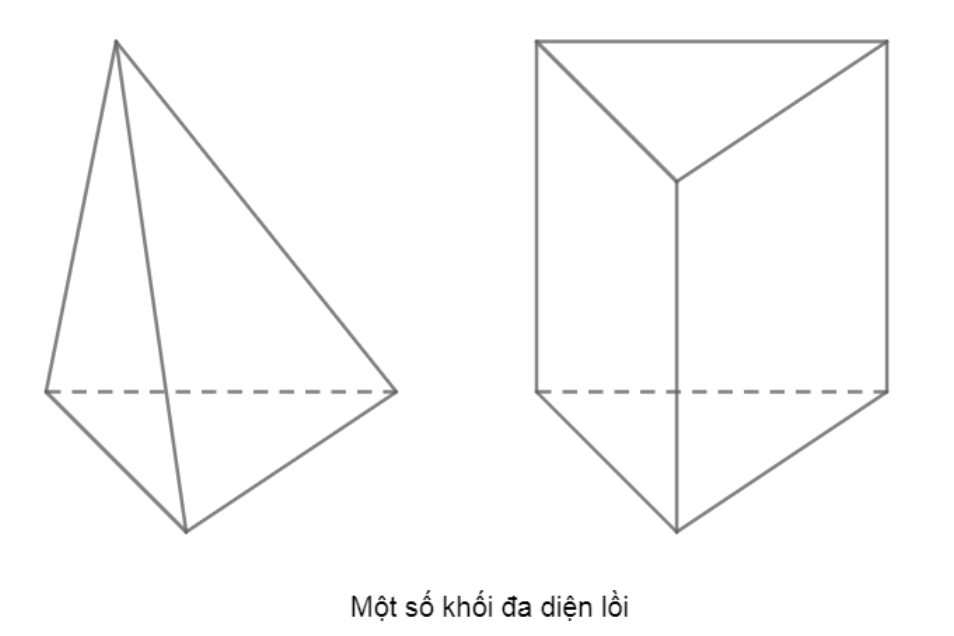
Công thức ƠLE: Trong một đa diện lồi nếu như gọi D là số đỉnh, C là số cạnh, M là số mặt ⇒ D − C + M = 2

c) Khối đa diện đều

Khối đa diện đều là khối đa diện lồi có những tính chất sau:

• Mỗi mặt của nó là một đa giác đều p cạnh.
• Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.

Khối đa diện đều như vậy được gọi là một khối đa diện đều loại 

Nhận xét: Các mặt của khối đa diện đều là các đa giác đều và bằng nhau.

Định lý: Chỉ có năm loại khối đa diện đều. Đó là các khối đa diện đều loại {3,3}; {4,3}; {3,4} và {3,5}

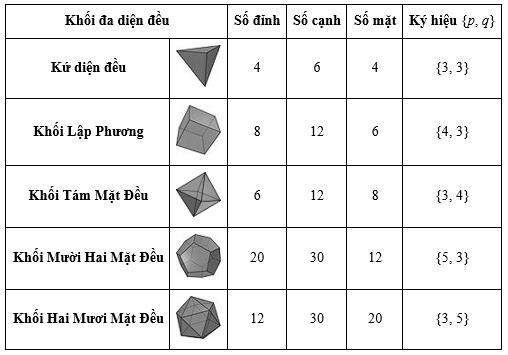
2. Thể tích khối đa diện

a) Thể tích khối chóp

– Nếu khối chóp đã cho có chiều cao h và diện tích đáy B ⇒ Thể tích tính theo công thức V = (B.h)/3

– Nếu khối chóp cần tính thể tích chưa biết chiều cao thì cần phải xác định được vị trí chân đường cao trên đáy.

• Chóp có cạnh bên vuông góc với chiều cao chính là cạnh bên.
• Chóp có hai mặt bên vuông góc với đáy đường cao là giao tuyến của hai mặt bên vuông góc đáy.
• Chóp có mặt bên vuông góc với đáy chiều cao của mặt bên vuông góc đáy.
• Chóp đều chiều cao hạ từ đỉnh tới tâm đa giác đáy.
• Chóp có hình chiếu vuông góc của một đỉnh xuống mặt đáy thuộc cạnh mặt đáy đường cao là từ đỉnh đến hình chiếu.

b) Thể tích khối lăng trụ

• Thể tích khối lăng trụ: V = B.h ( B là diện tích đáy, h là chiều cao)
• Thể tích khối hộp chữ nhật: V= a.b.c (a,b,c là ba kích thước)
• Thể tích khối lập phương: V = a³ (a là độ dài cạnh)

Chương 2: Mặt nón – Mặt trụ – Mặt cầu

1. Công thức:

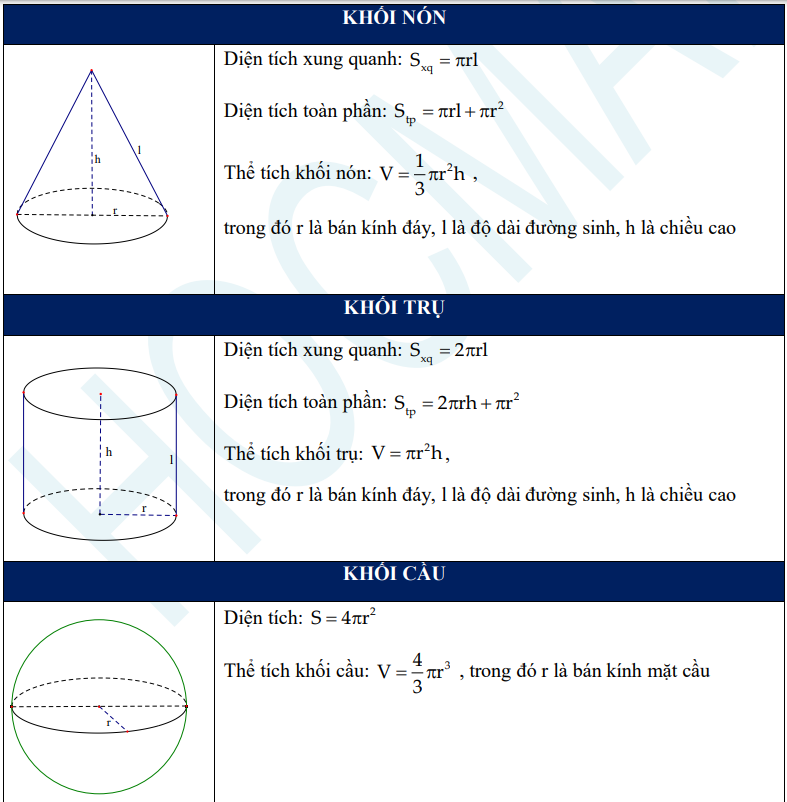
2. Một số định nghĩa, khái niệm

– Trục của đa giác đáy: là đường thẳng đi qua tâm của đường tròn ngoại tiếp của đa giác đáy và vuông góc cùng với mặt phẳng chứa đa giác đáy. Bất kì một điểm nào nằm ở trên trục của đa giác thì cách đều các đỉnh của đa giác ấy.

– Các bước xác định trục:

• Bước 1: Xác định tâm H của đường tròn ngoại tiếp với đa giác đáy.
• Bước 2: Qua H dựng vuông góc cùng với mặt phẳng đáy.

+) Đường trung trực của đoạn thẳng: là đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc cùng với đoạn thẳng đó. Bất kì một điểm nào nằm ở trên đường trung trực thì cách đều là hai đầu mút của đoạn thẳng.

+) Mặt trung trực của đoạn thẳng: là mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc cùng với đoạn thẳng đó. Bất kì một điểm nào nằm ở trên mặt phẳng trung trực thì cách đều hai đầu mút của đoạn thẳng.

+) Tâm mặt cầu ngoại tiếp hình đa diện: là điểm cách đều với các đỉnh của hình đa diện.

+) Bán kính mặt cầu: là khoảng cách từ I tới các đỉnh của hình đa diện.

Các dạng bài tập thường gặp:

• Dạng 1: Tính diện tích, thể tích và các yếu tố liên quan
• Dạng 2: Bài toán thiết diện
• Dạng 3: Mặt cầu ngoại tiếp khối đa diện

C. Đề ôn thi cuối kì 1 Toán 12 (Có hướng dẫn giải chi tiết)

Dưới đây là bộ đề thi gồm 05 đề thi học kỳ I Toán 12 do HOCMAI tổng hợp gửi đến các bạn. Để sử dụng bộ tài liệu tốt nhất, các bạn học sinh hãy photo ra giấy để có thể thực hành trực tiếp nhé!

Vậy là HOCMAI đã cùng các em học sinh ôn luyện lại toàn bộ Đề cương ôn thi học kì 1 Toán 12. HOCMAI chúc cho các em ôn luyện thi thật tốt, thật vững vàng khi ngồi trong phòng thi. Đừng quên truy cập hoctot.hocmai.vn để tham khảo thêm thật nhiều kiến thức, bài học bổ ích, những loại câu hỏi quan trọng nữa các em nhé!