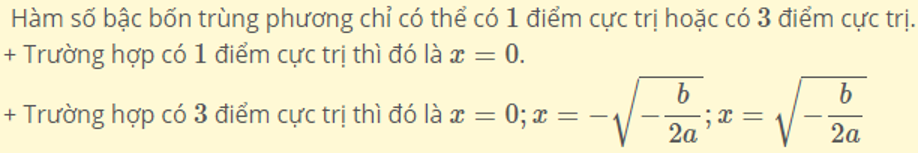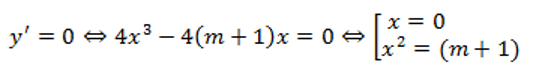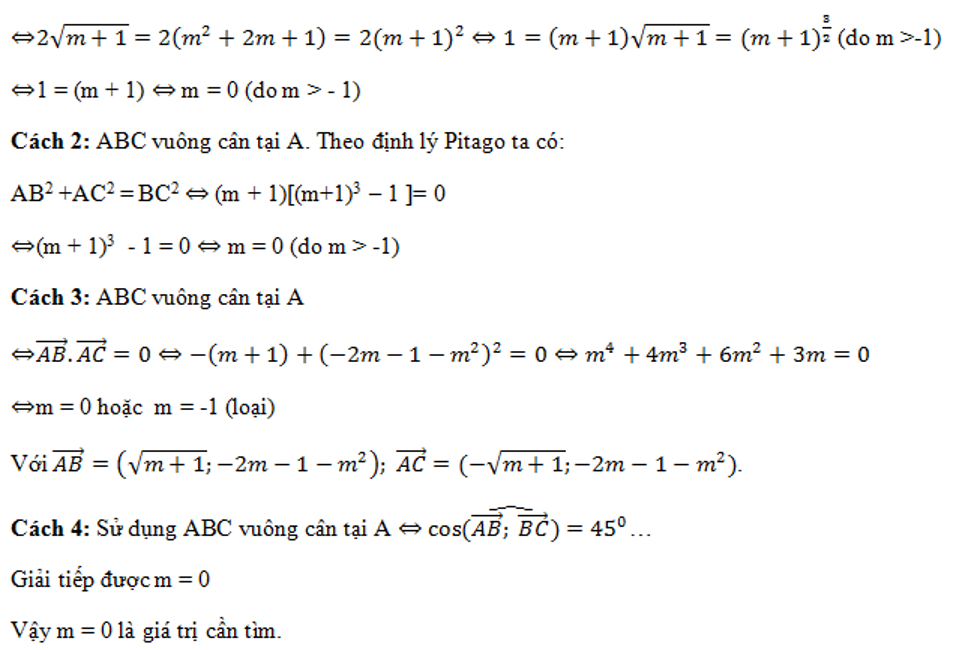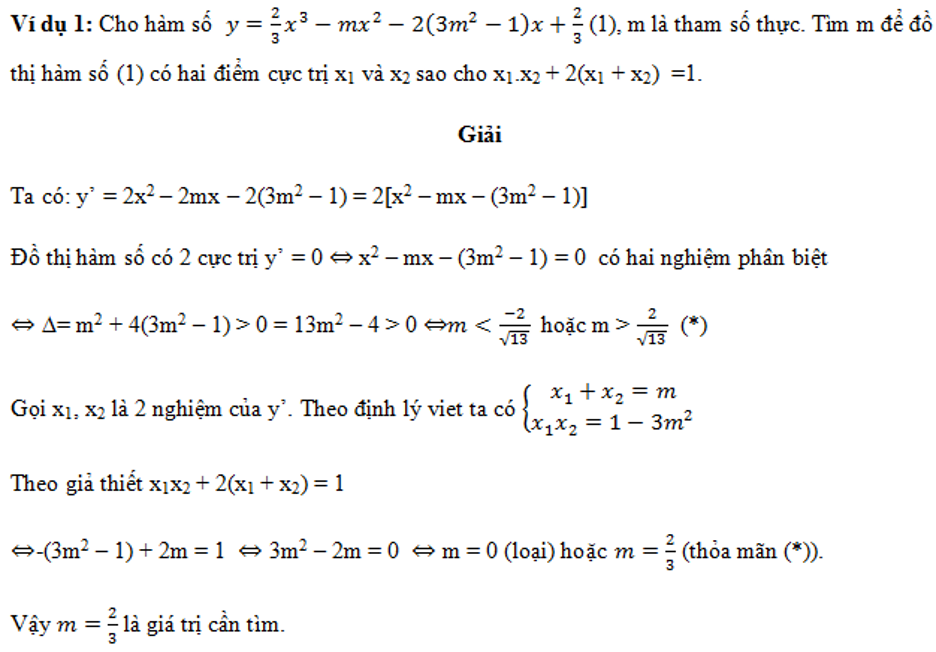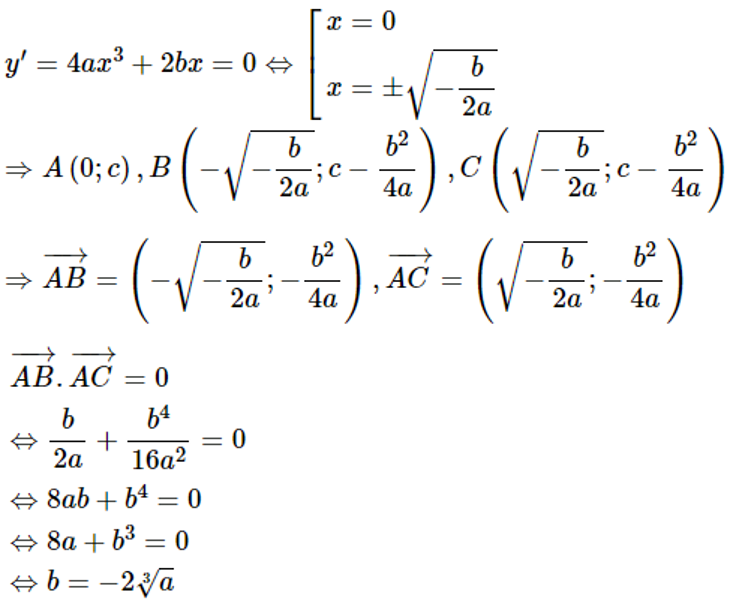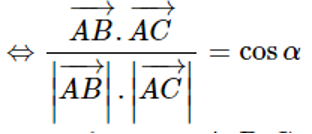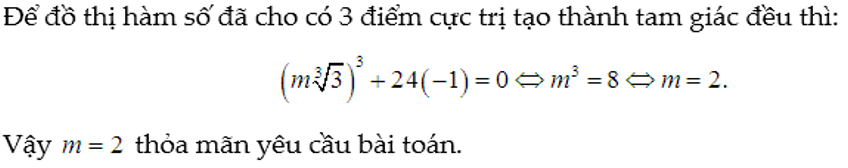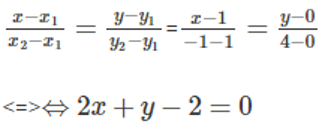Một số dạng toán về cực trị có tham số đối với các hàm số đơn giản:
Tham khảo thêm:
Dạng 1: Tìm điều kiện của tham số để hàm số bậc 3 có điểm cực trị
Phương pháp giải bài:
– Bước 1: Tính y′ của hàm số y.
– Bước 2: Nêu điều kiện để hàm số bậc 3 có điểm cực trị:
+ Hàm số có điểm cực trị khi và chỉ khi y′=0 có 2 nghiệm phân biệt ⇔Δ>0.
+ Hàm số không có điểm cực trị khi và chỉ khi y′=0 vô nghiệm hoặc có nghiệm kép ⇔Δ≤0
– Bước 3: Đưa ra kết luận.
Hàm số bậc 3 chỉ có thể có 2 cực trị hoặc không có điểm cực trị nào.
Dạng 2: Tìm điều kiện của tham số để hàm số bậc 4 trùng phương có điểm cực trị
Phương pháp giải bài:
– Bước 1: Tính y′.
– Bước 2: Nêu điều kiện để hàm số bậc 4 có điểm cực trị:
+ Hàm số có 1 điểm cực trị khi phương trình y′=0 có 1 nghiệm duy nhất.
+ Hàm số có 3 điểm cực trị khi phương trình y′=0 có 3 nghiệm phân biệt.
– Bước 3: Đưa ra kết luận.
Ví dụ: Cho hàm số y = x^4 – 2(m+1)x^2 + m^2 (1), với m là tham số thực. Tìm tham số m để đồ thị của hàm số (1) có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác vuông.
Giải
Đạo hàm y’ = 4x^3 – 4(m + 1)x.
Hàm số có 3 cực trị => m + 1=> 0 ⇔ m > -1
Khi đó đồ thị hàm số có 3 điểm cực trị:
Nhận xét: Vì A ∈ Oy, B và C đối xứng nhau qua Oy nên ∆ABC cân tại A nghĩa là AB = AC nên tam giác chỉ có thể vuông cân tại A.
Cách 1: Gọi M là trung điểm của BC=>M (0; -2m – 1)
Do đó để tam giác ABC vuông cân thì BC = 2AM (đường trung tuyến bằng nửa cạnh huyền)
Dạng 3: Tìm điều kiện của tham số để hàm số nhận điểm cho trước làm điểm cực trị
Phương pháp giải bài:
Ví dụ:
Dạng 4: Tìm điều kiện của tham số để đồ thị hàm số bậc 3 có 3 điểm cực trị thỏa mãn những điều kiện cho trước
Phương pháp giải bài:
– Bước 1: Tính y′
– Bước 2: Nêu điều kiện để đồ thị của hàm số có 2 điểm cực trị thỏa mãn điều kiện:
+ Đồ thị của hàm số có 2 điểm cực trị nằm về hai phía trục tung
⇔y′=0 có hai nghiệm phân biệt trái dấu ⇔ ac < 0
+ Đồ thị của hàm số có 2 điểm cực trị nằm cùng phía so với trục tung
+ Đồ thị hàm số có 2 điểm cực trị nằm về phía bên phải trục tung
+ Đồ thị hàm số có 2 điểm cực trị nằm về phía bên trái trục tung
+ Đồ thị của hàm số có 2 điểm cực trị A(x1;y1),B(x2;y2) thỏa mãn đẳng thức liên hệ giữa x1,x2 thì ta biến đổi đẳng thức đã cho làm xuất hiện x1+x2,x1.x2 rồi sử dụng hệ thức Vi-et để. ![]()
Dạng 5: Tìm điều kiện của tham số để đồ thị hàm số bậc 4 trùng phương có 3 điểm cực trị thỏa mãn những điều kiện cho trước
Phương pháp:
– Bước 1: Tính y′.
– Bước 2: Nêu điều kiện để đồ thị của hàm số có 3 điểm cực trị thỏa mãn điều kiện:
+ 3 điểm cực trị A,B,C trong đó điểm A(0;c) lập thành một tam giác vuông (vuông cân)
Khi đó:
Đây chính là công thức tính nhanh áp dụng trong các bài toán trắc nghiệm.
+ 3 điểm cực trị A,B,C trong đó A(0;c) tạo thành tam giác đều ⇔AB=BC=CA.
+ 3 điểm cực trị A,B,C trong đó A(0;c) tạo thành 1 tam giác có diện tích S0 cho trước
+ 3 điểm cực trị A,B,C trong đó A(0;c) tạo thành 1 tam giác có diện tích S0 lớn nhất
+ 3 điểm cực trị A,B,C trong đó A(0;c) tạo thành 1 tam giác cân có góc ở đỉnh bằng α cho trước
+ 3 điểm cực trị A,B,C trong đó A(0;c) tạo thành 1 tam giác có ba góc nhọn
– Bước 3: Đưa ra kết luận.
Ví dụ : Cho hàm số:
Tìm m để đồ thị của hàm số đã cho có 3 điểm cực trị tạo thành 1 tam giác đều.
Lời giải:
Dạng 6: Viết phương trình đi qua các điểm cực trị của đồ thị hàm số bậc 3
Phương pháp:
– Bước 1: Tính y′.
– Bước 2: Lấy y chia y′ ta được đa thức dư g(x)=mx+n
– Bước 3: Đưa ra kết luận: y=mx+n là đường thẳng cần tìm.
Ví dụ:
Viết phương trình đi qua 2 điểm cực trị của đồ thị hàm số y=x^3−3x+2
Giải:
Ta có: y‘=3x^2−3
Hoành độ 2 điểm cực trị là nghiệm của phương trình:y‘=0
y‘=0⇔3x^2−3=0
Vậy x1=1 và y1=0
hoặc x2=−1 và y2=4
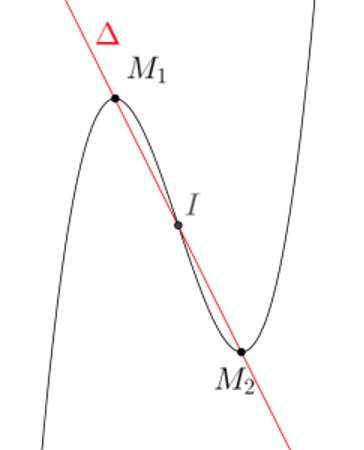
Vậy hai điểm cực trị là M1=(1;0), M2=(−1;4)
Phương trình đường thẳng Δ đi qua 2 điểm cực trị là:
Tham khảo thêm: