Kỳ thi cuối học kì 1 đang ngày càng đến gần, các em học sinh cần ôn thi đúng trọng tâm để chuẩn bị tốt nhất cho kỳ thi này. Đề cương ôn thi học kì 1 Toán 11 được BUTBI biên soạn tổng hợp đầy đủ kiến thức cần nắm vững, các dạng bài tập và câu hỏi có khả năng xuất hiện ở trong đề thi HK1 Toán học lớp 11 sắp tới. Các em tham khảo ngay sau đây nhé!
⇒ Tham khảo thêm:
- Đề cương ôn thi học kì 1 môn Hóa lớp 11
- Đề cương ôn thi học kì 1 môn Lý lớp 11
- Đề cương ôn thi học kì 1 môn Sinh lớp 11
- Đề cương ôn thi học kì 1 môn Ngữ Văn lớp 11
- Đề cương ôn thi học kì 1 Tiếng Anh lớp 11
A. KIẾN THỨC TRỌNG TÂM ĐẠI SỐ – ÔN THI HỌC KÌ 1 TOÁN LỚP 11
Chương 1: Hàm số lượng giác và phương trình lượng giác
I – Hàm số lượng giác
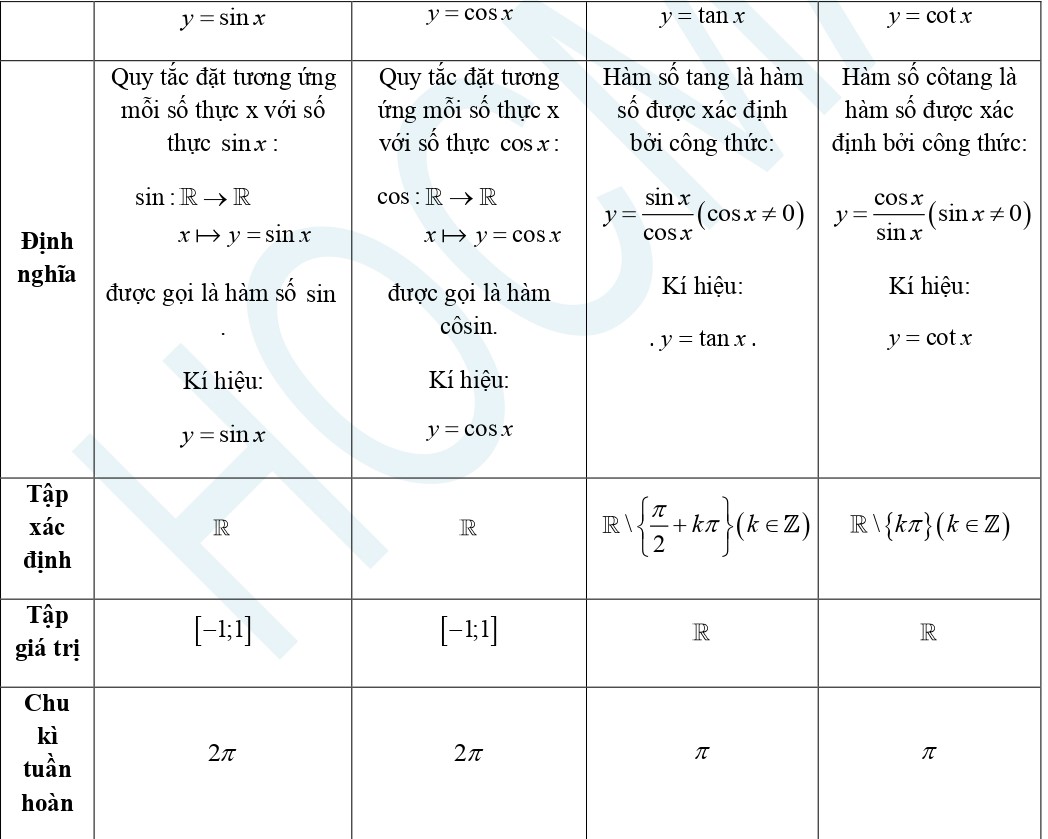
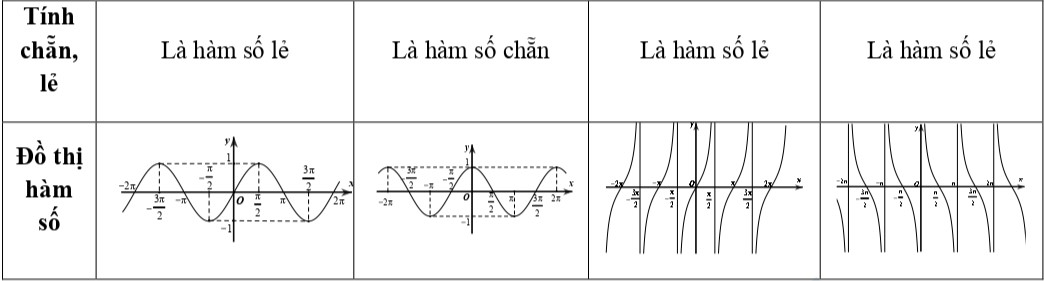
II – Phương trình lượng giác

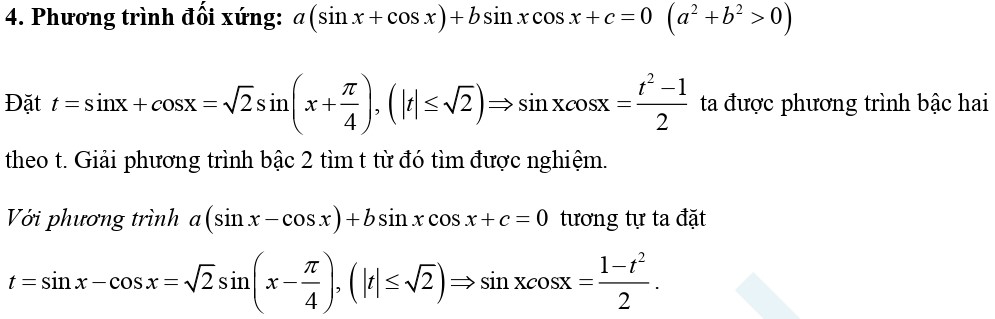
III – Một số dạng bài thường gặp
Dạng 1: Tìm tập xác định của hàm số lượng giá
Phương pháp giải:
Tìm điều kiện để hàm số có nghĩa
Giải điều kiện và rút ra kết luận
Chú ý: Với các hàm chứa căn bậc chẵn thì biểu thức dưới dấu căn phải ≥ 0 ; các hàm phân thức thì mẫu số phải ≠ 0 ; các hàm liên quan đến tan,cot thì sin hoặc cos phải ≠ 0;…

Dạng 2: Tìm tập giá trị của hàm số lượng giác
Phương pháp giải:
Sử dụng các công thức lượng giác đưa hàm số về hàm chỉ chứa một hàm lượng giác.
Đặt ẩn phụ đưa về phương trình bậc nhất với sinx và cosx để tìm giá trị lớn nhất, nhỏ nhất của hàm số. Từ đó suy ra tập giá trị của hàm số lượng giác đã cho.

Dạng 3: Xác định tính chẵn, lẻ của hàm số lượng giác
Phương pháp giải:
- Tìm tập xác định D của hàm số
- Với x ∈ D ⇔ -x ∈ D
- Tính f (-x): Nếu f(x) = f(-x), với mọi x ∈ D thì hàm số chẵn. Nếu f(-x) = -f(x), với mọi x ∈ D thì hàm số lẻ.

Dạng 4: Xác định chu kì tuần hoàn của hàm số lượng giác
Phương pháp giải:
Áp dụng cách tính chu kì sau:
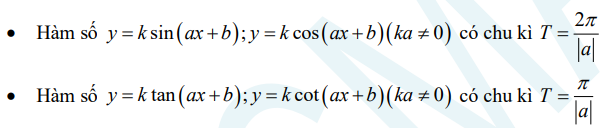
Ví dụ:

Dạng 5: Xác định các yếu tố về nghiệm của phương trình lượng giác
Phương pháp giải:
Nắm vững các phương pháp giải phương trình lượng giác đã học.
Để xác định nghiệm thuộc khoảng (đoạn, nửa khoảng) cho trước ta cần tìm nghiệm của phương trình và cho nghiệm thuộc khoảng (đoạn, nửa khoảng) theo yêu cầu. Từ đó tìm được các giá trị nguyên của k và nghiệm của phương trình.
Lưu ý khi giải phương trình lượng giác cần tìm điều kiện của phương trình (nếu có) và sau khi giải ra nghiệm cần đối chiếu với điều kiện.

Dạng 6: Xác định tham số m để phương trình thỏa mãn điều kiện cho trước
Phương pháp giải:
Dùng phương pháp đặt ẩn số phụ ta có thể đưa một phương trình lượng giác thành một phương trình đại số.
Đặt t = f(x)
Tìm điều kiện cho ẩn số phụ t
Biến đổi phương trình đã cho thành một phương trình đã biết cách giải như phương trình bậc hai, bậc ba theo t.
Ngoài ra, có thể sử dụng các phương pháp khác như sử dụng các phép biến đổi tương đương đưa về phương trình đã học rồi sử dụng điều kiện có nghiệm của các phương trình,…

Chương 2: Tổ hợp – Xác suất
I – Hoán vị – Chỉnh hợp – Tổ hợp

II – Xác suất
1. Quy tắc cộng xác suất
Hai biến cố A và B được gọi là xung khắc nhau nếu chúng không đồng thời xảy ra trong một phép thử.
Quy tắc cộng xác suất:
Nếu A và B xung khắc, thì P (A∪B) = P(A) + P(B)
Nếu các biến cố A1, A2 A,3,…. A k xung khắc nhau thì
P(A1∪ A2 ∪…. ∪ Ak) = P(A1) + P(A2) + … + P(Ak)
2. Quy tắc nhân xác suất
Hai biến cố gọi là độc lập: nếu việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra biến cố kia.
Quy tắc nhân xác suất: Nếu A và B là hai biến cố độc lập nhau thì P(A.B) = P(A).P(B)
III – Một số dạng bài thường gặp
Dạng 1: Bài toán đếm
Phương pháp giải:
Đếm trực tiếp: Dựa vào yêu cầu của đề bài, ta phân ra các trường hợp và sử dụng các quy tắc đếm để tính toán trong từng trường hợp. Kết quả bài toán là tổng các phương án đếm trong các trường hợp trên.
Đếm gián tiếp: Ta đếm số phương án thực hiện hành động H là a và đếm số phương án thực hiện hành động H nhưng không thỏa mãn tính chất T là b. Số phương án hành động H và thỏa mãn yêu cầu bài toán là a – b.

Dạng 2: Phương trình – bất phương trình tổ hợp
Phương pháp giải:
Áp dụng công thức và tính chất liên quan đến hoán vị, chỉnh hợp, tổ hợp.

Dạng 3: Tìm số hạng, hệ số chứa x^a trong khai triển
Phương pháp giải:
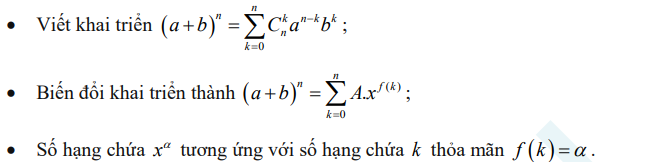
Ví dụ:



Ví dụ: Một công ty may mặc có hai hệ thống máy chạy song song. Xác suất để hệ thống máy thứ nhất hoạt động tốt là 90%, xác suất để hệ thống máy thứ hai hoạt động tốt là 80%. Công ty chỉ có thể hoàn thành đơn hàng đúng hạn nếu ít nhất một trong hai hệ thống máy hoạt động tốt. Xác suất để công ty hoàn thành đúng hạn là A) 98%.
B) 2%.
C) 80%.
D) 72%.
Lời giải:

Chương 3: Dãy số – Cấp số cộng và cấp số nhân
I – Dãy số
1) Dãy số tăng, dãy số giảm
Định nghĩa:

II – Cấp số cộng – Cấp số nhân
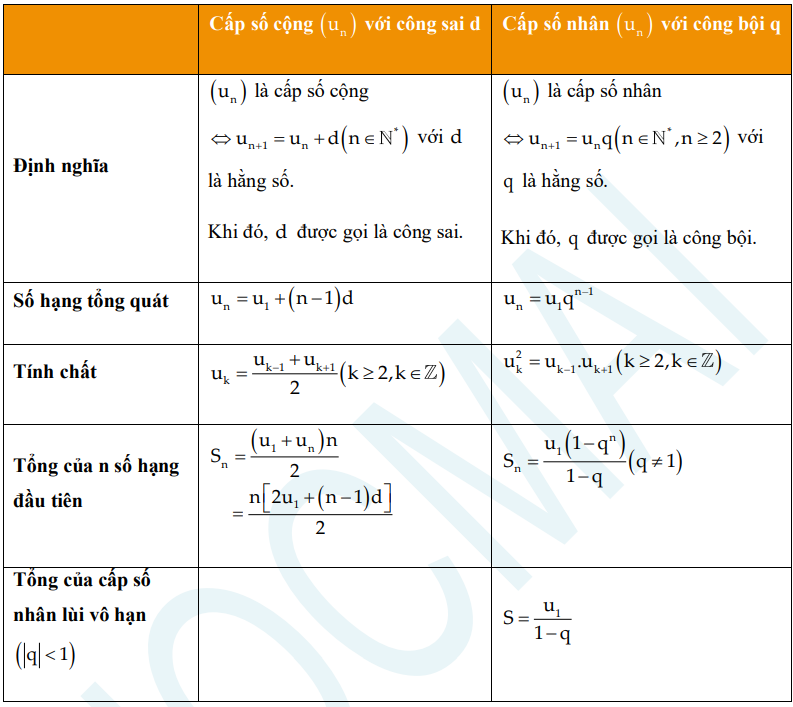
III – Một số dạng bài thường gặp
Dạng 1. Xác định số hạng, số hạng tổng quát của dãy số
Phương pháp giải:
1. Xác định số hạng của dãy số
Thay trực tiếp giá trị của n vào công thức hoặc tính lần lượt các số hạng,…
2. Xác định số hạng tổng quát của dãy số
Cách 1. Sử dụng biến đổi đại số để thu gọn và đơn giản biểu thức của Un
Cách 2. Sử dụng phương pháp quy nạp bằng việc thực hiện theo các bước sau:
Viết một vài số hạng đầu của dãy, từ đó dự đoán công thức cho Un
Chứng minh công thức dự đoán bằng phương pháp quy nạp

Dạng 2: Xét tính tăng giảm, bị chặn của dãy số
Phương pháp giải:


Dạng 3: Xét một dãy số có là cấp số cộng/cấp số nhân hay không?
Phương pháp giải:

Ví dụ:



Dạng 6: Ứng dụng cấp số cộng, cấp số nhân vào thực tế
Phương pháp giải:
Bước 1: Từ các dữ kiện của đề bài, xây dựng công thức số hạng tổng quát (hoặc dãy các số hạng)
Bước 2: Xác định dãy các số hạng là cấp số cộng hay cấp số nhân. Tìm số hạng đầu, công sai hoặc công bội.
Bước 3: Tính kết quả theo yêu cầu bài toán

B. KIẾN THỨC TRỌNG TÂM HÌNH HỌC – ÔN THI HỌC KÌ 1 TOÁN LỚP 11
Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
Kiến thức trọng tâm:
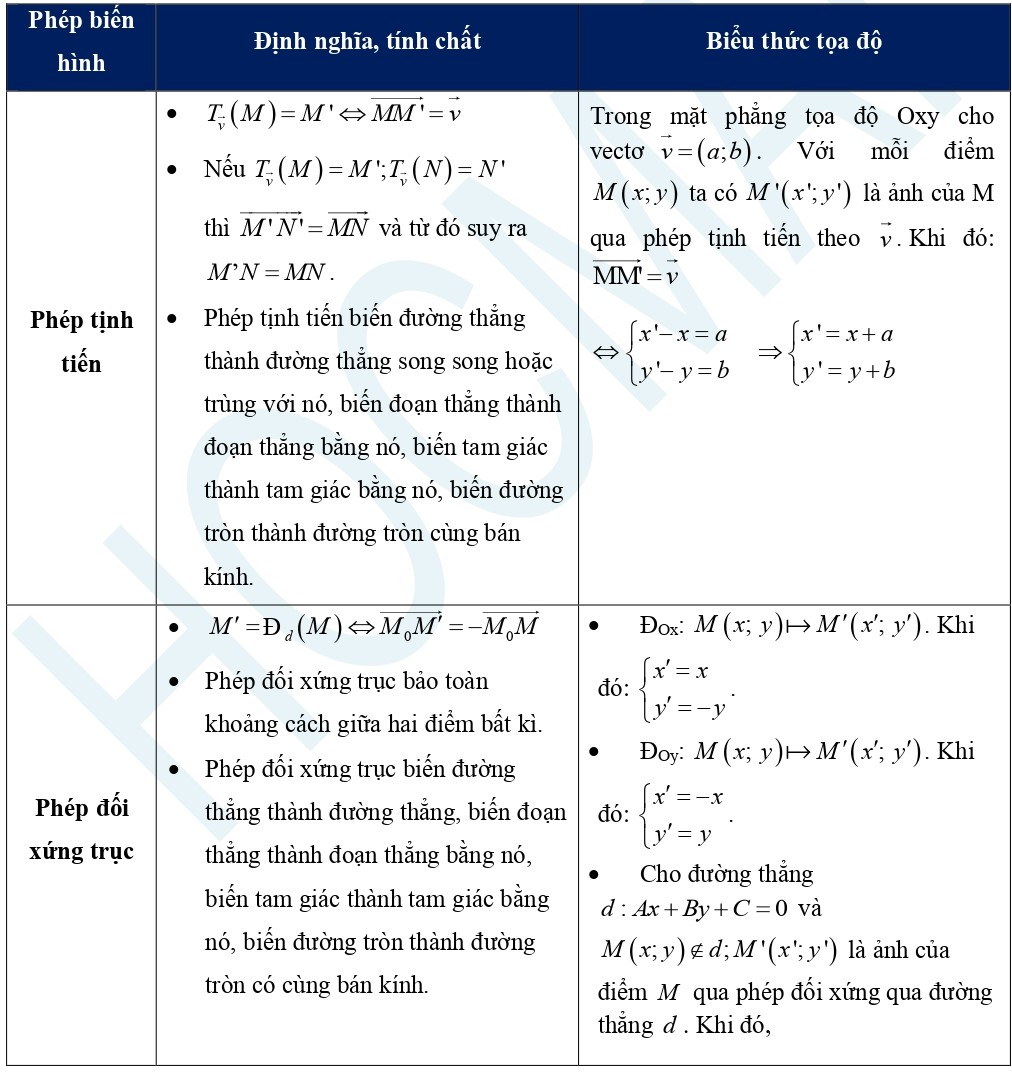

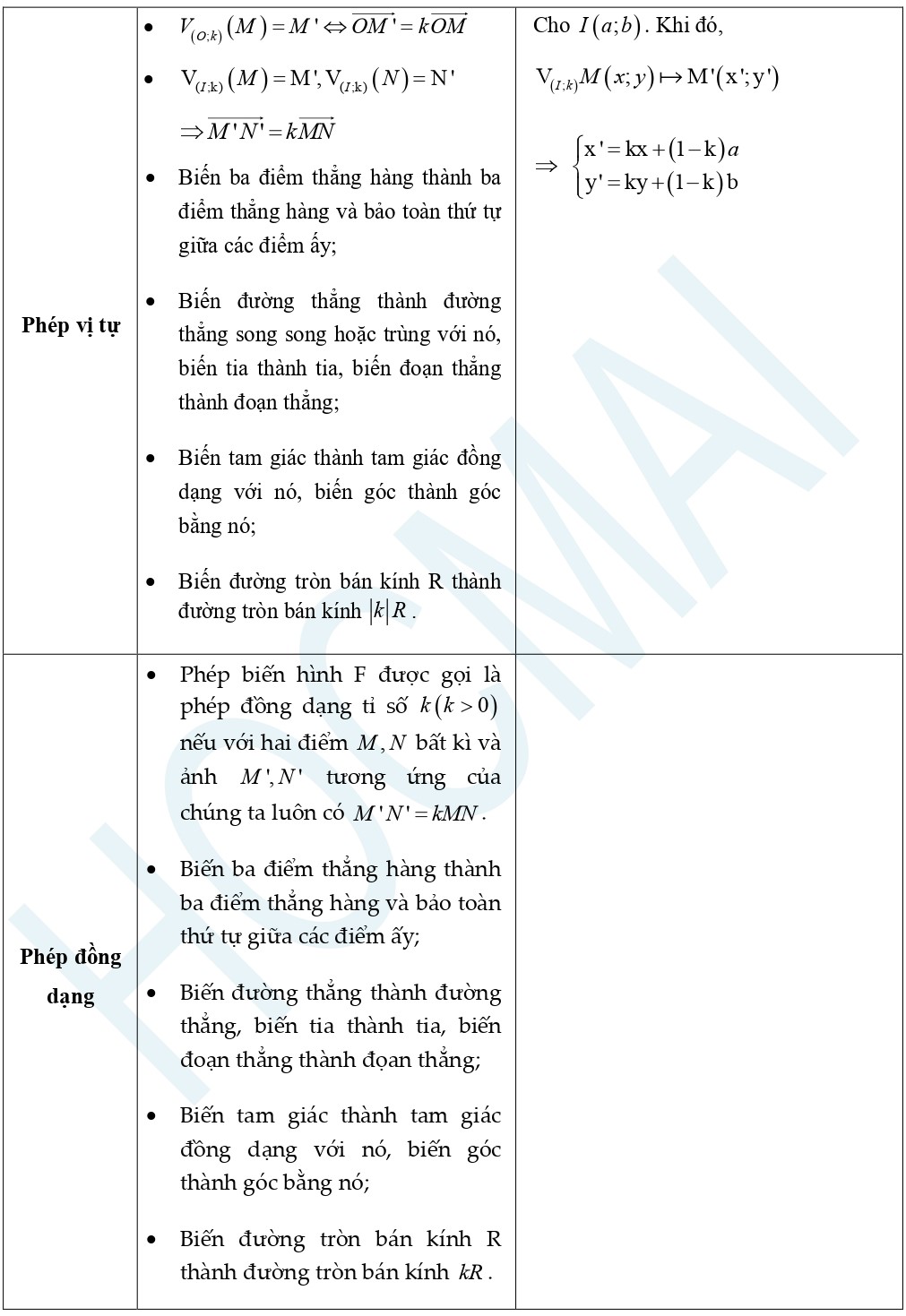
Dạng 1: Chứng minh/xác định ảnh (điểm, đường thẳng,…) qua phép biến hình
Phương pháp giải:
Áp dụng định nghĩa và tính chất của phép biến hình kết hợp với dữ kiện đề bài.

Dạng 2: Tìm tọa độ điểm, phương trình đường thẳng,… qua phép biến hình
Phương pháp giải:
Áp dụng công thức phần biểu thức tọa độ.

Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
I – Các tính chất thừa nhận
Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Tính chất 4: Tồn tại bốn điểm không cùng thuộc một mặt phẳng.
Tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.
Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng sẽ có một đường thẳng chung đi qua điểm chung ấy.
Tính chất 6: Trên mỗi mặt phẳng, các kết đã biết trong hình học phẳng đều đúng.
Định lí: Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
II – Cách xác định một mặt phẳng
Có ba cách xác định một mặt phẳng:
Một mặt phẳng được hoàn toàn xác định nếu biết nó đi qua ba điểm A,B,C không thẳng hàng. Kí hiệu: (ABC).
Một mặt phẳng được xác định nếu biết nó đi qua một điểm A và chứa một đường thẳng d không đi qua điểm đó. Kí hiệu: (A,d).
Một mặt phẳng được xác định nếu biết nó chứa hai đường thẳng a,b cắt nhau. Kí hiệu: (a,b).
III – Một số hình đa diện
1. Hình chóp và tứ diện

Nếu đáy của hình chóp là một miền tam giác, tứ giác, ngũ giác,… thì hình chóp tương ứng gọi là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác,…
Chú ý:
Hình chóp tam giác còn được gọi là hình tứ diện.
Hình tứ diện có bốn mặt là những tam giác đều hay có tất cả các cạnh bằng nhau được gọi là hình tứ diện đều.
2. Hình lăng trụ và hình hộp
Định nghĩa hình lăng trụ:
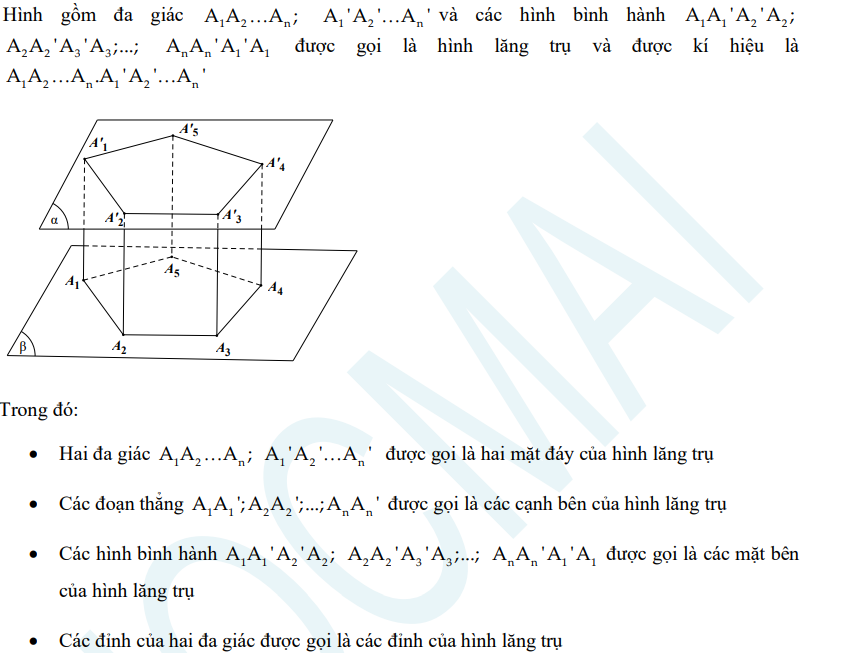
Nhận xét:
Các cạnh bên của hình lăng trụ song song và bằng nhau.
Các mặt bên của hình lăng trụ là các hình bình hành.
Hai đáy của hình lăng trụ là hai đa giác bằng nhau.
Tùy theo đa giác đáy, ta có hình lăng trụ tam giác, lăng trụ tứ giác,…
Định nghĩa hình hộp:
– Hình lăng trụ có đáy là hình bình hành gọi là hình hộp.
– Hình hộp có tất cả các mặt bên và các mặt đáy đều là hình chữ nhật gọi là hình hộp chữ nhật.
– Hình hộp có tất cả các mặt bên và các mặt đáy đều là hình vuông gọi là hình lập phương.
3. Hình chóp cụt
Định nghĩa:
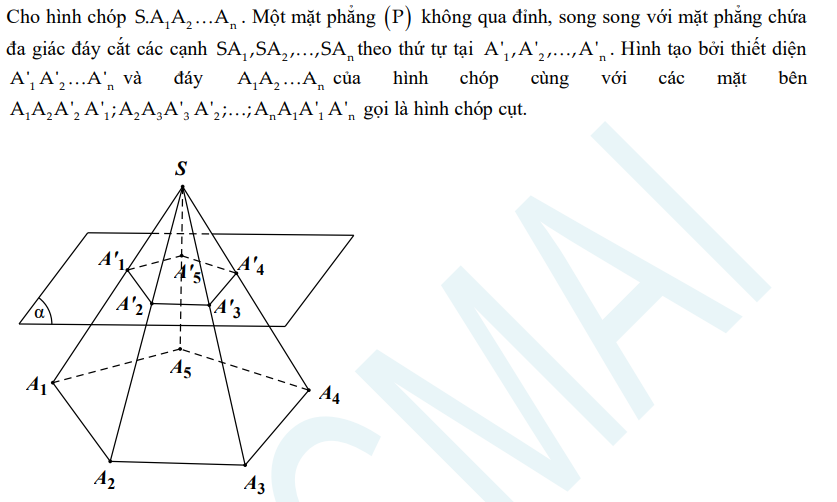
Tính chất:
- Hai đáy là hai đa giác có các cạnh tương ứng song song và các tỉ số các cặp cạnh tương ứng bằng nhau.
- Các mặt bên của hình chóp cụt là các hình thang.
- Các đường thẳng chứa các cạnh bên đồng quy tại một điểm.
IV – Thiết diện
Thiết diện của hình (H) và hình (Q) là phần chung nhau giữa 2 hình đó.
Thiết diện của mặt phẳng (α) với hình chóp (H) là phần chung giữa mặt phẳng (α) và hình chóp (H) .
Đặc điểm của thiết diện:
- Thiết diện là đa giác kín.
- Các cạnh của thiết diện nằm trên các mặt của hình đa diện.
- Cạnh của thiết diện được hình thành từ những đoạn giao tuyến của mặt phẳng cắt với các mặt của hình đa diện.
- Trong giới hạn hình đa diện thì thiết diện có thể cắt hoặc không cắt tất cả các mặt của hình chóp.
V – Vị trí tương đối

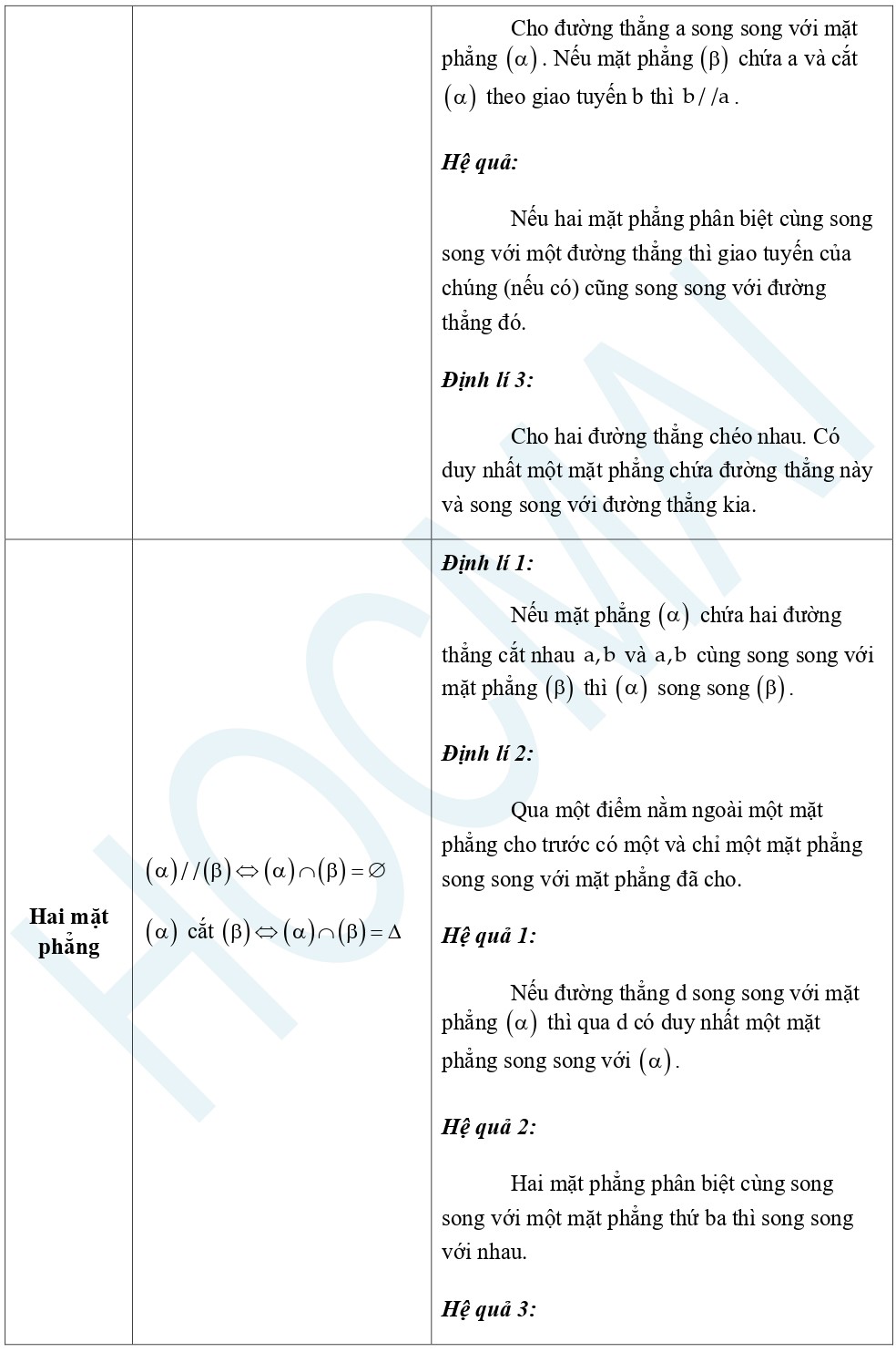

VI – Định lí Ta – lét trong không gian
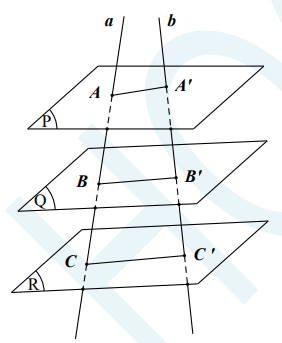
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
VII – MỘT SỐ DẠNG BÀI THƯỜNG GẶP
Dạng 1: Chứng minh song song
Phương pháp giải:
- Chứng minh hai đường thẳng song song

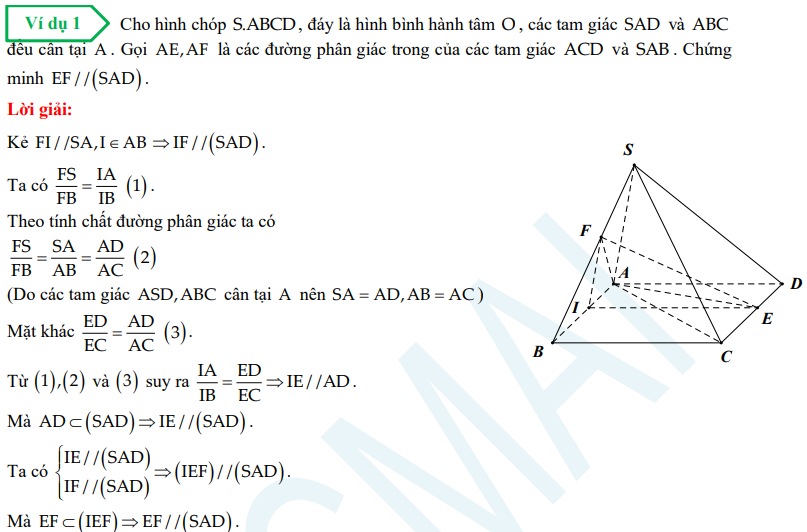
Dạng 2: Xác định thiết diện
Phương pháp giải:
Xác định điểm chung có trước
Từ các điểm chung có trước ta xác định giao tuyến của mặt phẳng với các mặt chứa điểm chung đó.
Từ giao tuyến đó ta xác định đoạn giao tuyến bằng cách tìm giao điểm của giao tuyến với các cạnh của mặt phẳng đó.
Từ giao tuyến tìm được ta tiến hành tìm giao tuyến và các đoạn giao tuyến còn lại cho đến khi được 1 hình kín.
Lưu ý:
Nếu hai mặt phẳng (α);(β) có điểm chung M và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của (α);(β) là đường thẳng qua M và song song với d và d’.


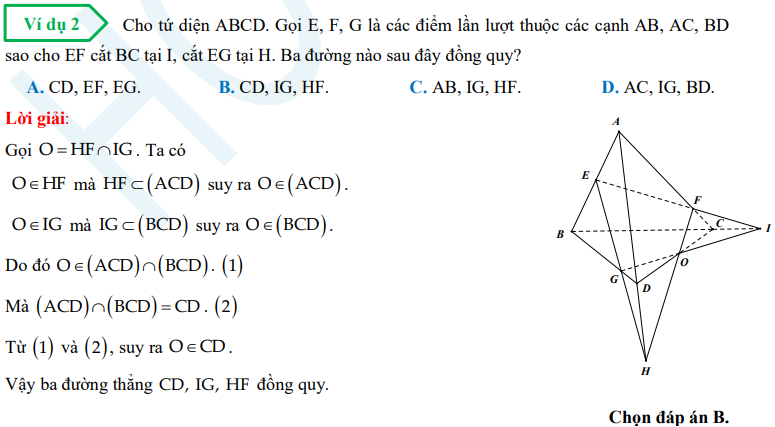
Dạng 3: Chứng minh thẳng hàng, đồng quy, đồng phẳng
Phương pháp giải:
Để chứng minh ba điểm thẳng hàng ta chứng minh chúng cùng thuộc giao tuyến của hai mặt phẳng, tức là:
Xác định d = (α) ∩ (β)
Chứng minh d đi qua ba điểm A,B,C hoặc chứng minh AB đi qua C. Từ đó, suy ra A,B,C thẳng hàng.
Để chứng minh ba đường thẳng đồng quy, ta chứng minh giao điểm của hai đường thẳng này thuộc đường thẳng kia hoặc áp dụng định lí về giao tuyến của hai mặt phẳng.
Để chứng minh 4 điểm A,B,C,D đồng phẳng, ta cần:
Xác định đường thẳng a,b lần lượt đi qua hai trong 4 điểm.
Chứng minh a,b song song hoặc cắt nhau. Khi đó, 4 điểm A,B,C,D đồng phẳng.
C. ĐỀ ÔN THI CUỐI HỌC KÌ I MÔN TOÁN LỚP 11 (CÓ ĐÁP ÁN CHI TIẾT)
Sau đây là tổng hợp bộ tài liệu gồm 03 đề ôn thi học kỳ I môn Toán lớp 11 có lời giải chi tiết do BUTBI tổng hợp. Để sử dụng bộ tài liệu tốt nhất, các em học sinh hãy in ra giấy rồi làm bài trực tiếp nhé!
Trên đây là Đề cương ôn thi học kì 1 Toán 11 tổng hợp đầy đủ kiến thức trọng tâm cũng như các dạng bài thường xuất hiện trong đề kiểm tra cuối HK1. Các em hãy ôn luyện thật chăm chỉ để đạt được kết quả cao trong kỳ thi sắp tới nhé!