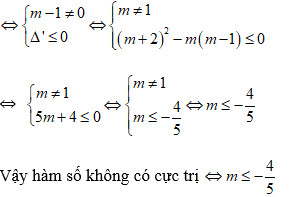Tìm m để hàm số không có cực trị (hàm số bậc 3) có lời giải để các bạn tham khảo.
KHÓA ÔN CHUYÊN ĐỀ THI TỐT NGHIỆP THPT
NHANH CHÓNG LẤP LỖ HỔNG KIẾN THỨC - TỰ TIN NHẬP CUỘC ĐƯỜNG ĐUA ĐẠI HỌC
✅ Hệ thống hóa kiến thức trọng tâm theo từng chuyên đề thi tốt nghiệp THPT
✅ Cung cấp các phương pháp làm bài hiệu quả theo từng chuyên đề THPT
✅ Lưu ý các lỗi sai thường gặp và tips, mẹo gia tăng tốc độ làm bài
✅ Đầy đủ các môn Toán - Lí - Hóa - Anh - Văn - Sinh - Sử - Địa - GDCD
✅ Học phí chỉ 50K/chuyên đề
Tham khảo thêm:
Cách tìm m để hàm số không có cực trị
Xét hàm số sau: y = ax3 + bx2 + cx + d với a ≠ 0
Khi đó y’ = 3ax2 + 2bx+c với y’ = 0 ⇔ 3ax2 + 2bx+c=0
Hàm số không có cực trị khi và chỉ khi phương trình y’ = 0 vô nghiệm hoặc là có nghiệm kép ⇔ Δ’ ≤ 0 ⇔ b2-3ac ≤ 0
Tìm m để hàm số không có cực trị – Bài tập
Tìm m để hàm số không có cực trị (ví dụ 1)
Tìm tổng số giá trị nguyên của m để hàm số
không có cực trị:
- A. 5
- B. 3
- C. 4
- D. 7
Lời giải chi tiết
Đáp án đúng: A
Ta có y’ = x2 + 2mx – (2m – 3)
Xét y’ = 0 ⇔ x2 + 2mx – (2m – 3) = 0
Hàm số đã không có cực trị khi vài chỉ khi y’ = 0 có tối đa 1 nghiệm
⇔ Δ’ ≤ 0 ⇔ m2 + (2m – 3) ≤ 0 ⇔ -3 ≤m≤ 1
Kết hợp với điều kiện m nguyên nên m{-3;-2;-1;0;1}
Vậy sẽ có 5 giá trị m thỏa mãn yêu cầu bài toán.
Tìm m để hàm số không có cực trị (ví dụ 2)
Với giá trị nào của tham số m thì hàm số y = x3 – 3x2 + 3(1 – m2)x + 1 sẽ không có cực trị.
- A. m ≠ 2
- B. m ∈ R
- C. m = 0
- D. Không tồn tại m
Lời giải chi tiết
Đáp án đúng: C
Ta có y’ = 3x2 – 6x + 3(1 – m2) với y’ = 0 ⇔ x2-2x + 1 – m2 = 0
Hàm số đã cho sẽ không có điểm cực trị khi phương trình y’ = 0 vô nghiệm hoặc có nghiệm kép ⇔ Δ’ ≤ 0 ⇔ 1 – (1 – m2) ≤ 0 ⇔ m2 ≤ 0 vậy m=0 thỏa mã yêu cầu bài toán.
Tìm m để hàm số không có cực trị (ví dụ 3)
Cho hàm số sau: y = -2x3+(2m – 1)x2-(m2 – 1)x – 2. Tìm tất cả các giá trị của tham số m để hàm số đã cho sẽ không có cực trị .
Lời giải chi tiết
Chúng ta có y’ = -6x2 + 2(2m – 1)x – (m2 – 1) với y’ = 0 ⇔ -6x2 + 2(2m – 1)x – (m2 – 1) = 0
Hàm số đã cho sẽ không có cực trị khi phương trình y’ = 0 có vô nghiệm hoặc là có nghiệm kép
Tìm m để hàm số không có cực trị (ví dụ 4)
Tìm tất cả các giá trị của tham số m để hàm số 
sẽ không có cực trị.
Lời giải chi tiết
– Với trường hợp m=1 hàm số đã cho sẽ trở thành y = 3x2 + x + 2 đây là hàm số bậc hai nên luôn chỉ có duy nhất 1 cực trị.
→ Vậy với m=1 (loại)
– Trường hợp m ≠ 1, có y’ = (m – 1)x2 + 2(m + 2)x + m với y’ = 0 ⇔ (m – 1)x2 + 2(m + 2)x + m = 0
Hàm số đã cho sẽ không có cực trị khi phương trình y’ = 0 vô nghiệm hoặc là có nghiệm kép
Trên đây là một số bài tập Tìm m để hàm số không có cực trị có lời giải (toán 12) để các bạn tham khảo.
