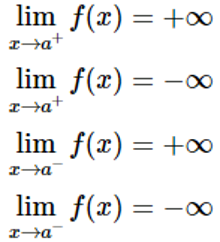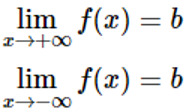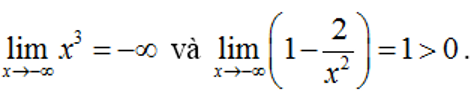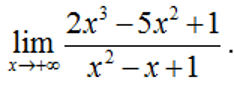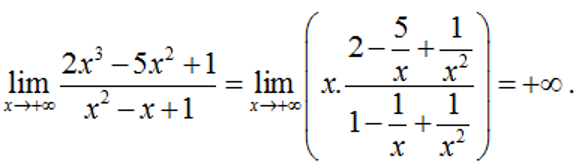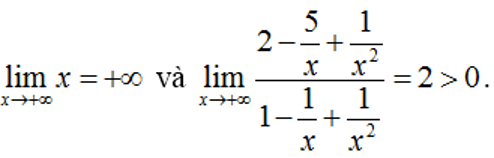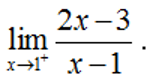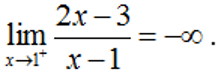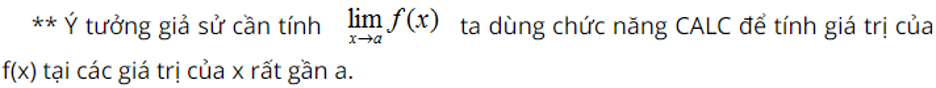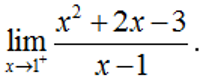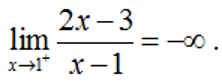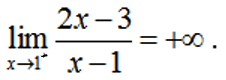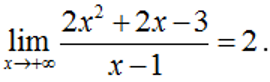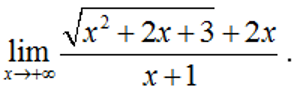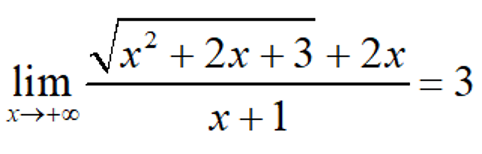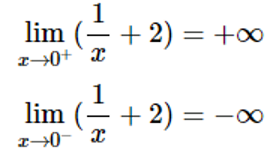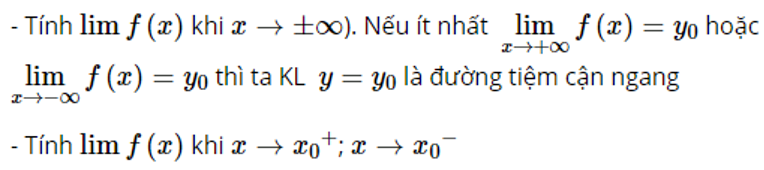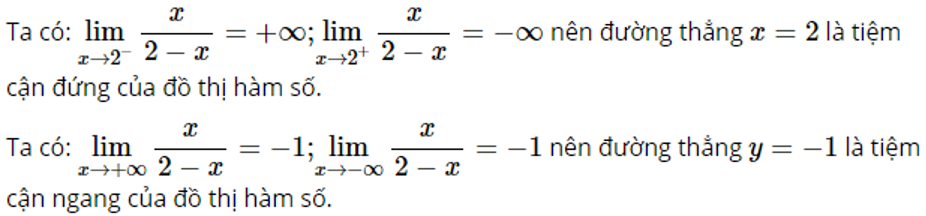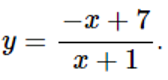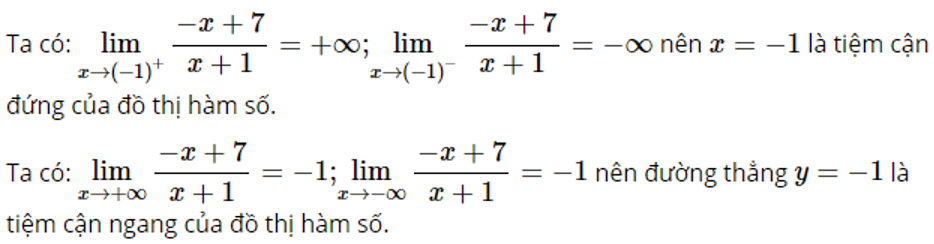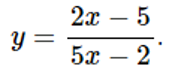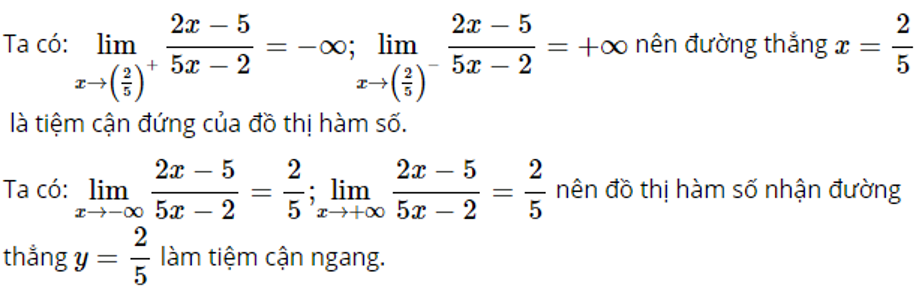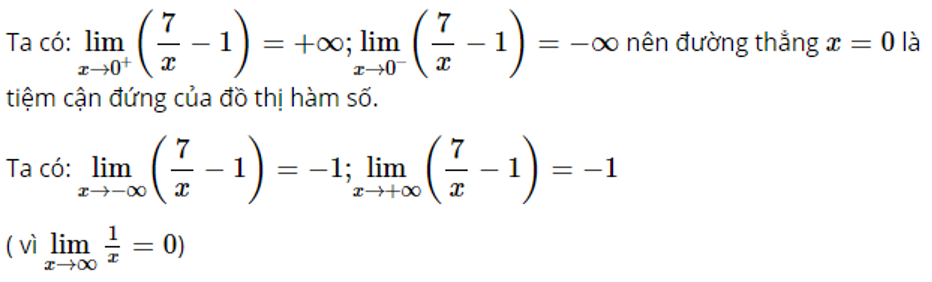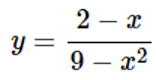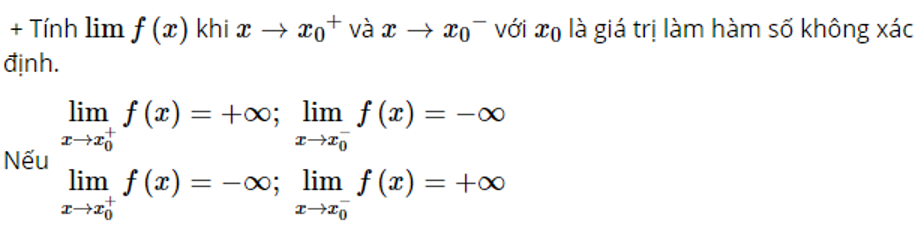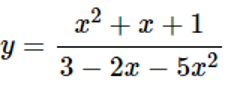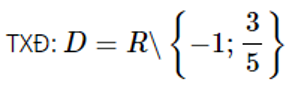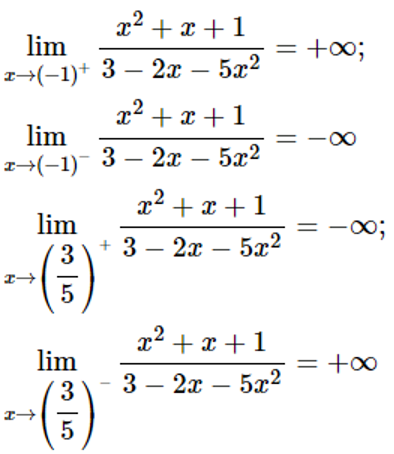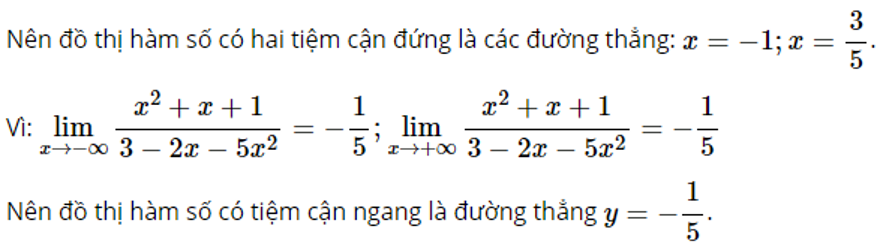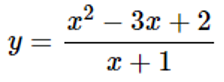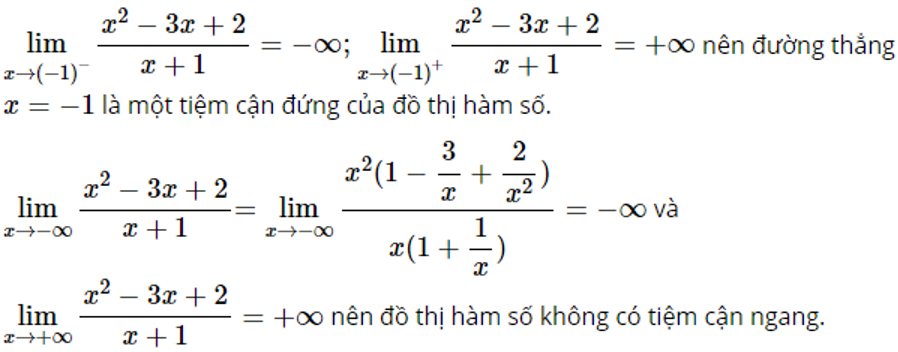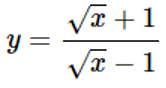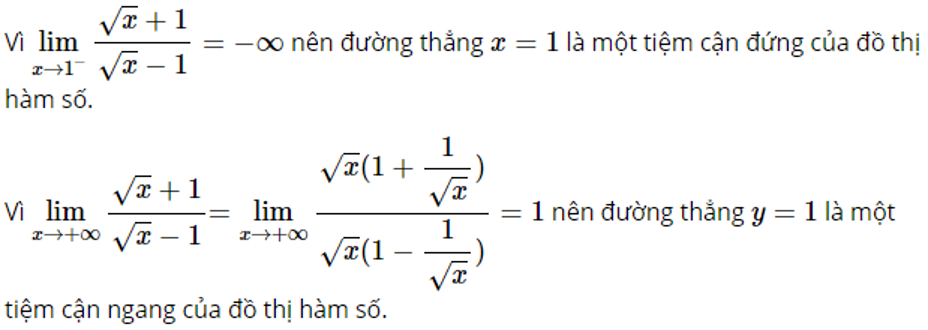Giải toán đại số 12 bài 4 đường tiệm cận. Nội dung bài học dưới đây sẽ giúp các bạn nắm được khái niệm tiệm cận của đồ thị hàm số, biết được các phương pháp để tìm đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số, cùng với một số những ví dụ minh họa giúp các bạn biết cách giải bài tập từ cơ bản đến nâng cao.

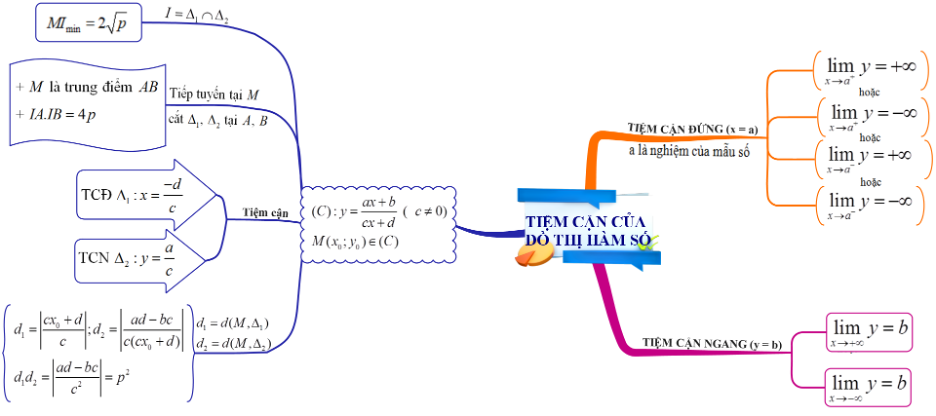
Tham khảo thêm:

• Giá trị lớn nhất nhỏ nhất của hàm số
• Giải bài tập toán 12

A: Lý thuyết đường tiệm cận

1. Tiệm cận đứng

Đường thẳng x=a là đường tiệm cận đứng của (C) nếu như ít nhất một trong bốn điều kiện sau đây được thoả mãn:

2. Tiệm cận ngang

Đường thẳng y=b là tiệm cận ngang của (C) nếu như ít nhất một trong các điều kiện sau đây được thỏa mãn:

Chú ý:

– Đồ thị của hàm đa thức không có tiệm cận đứng và tiệm cận ngang, do đó trong các bài toán khảo sát và vẽ đồ thị của hàm đa thức, ta không cần phải tìm các tiệm cận này.

3. Tiệm cận xiên

B. Kĩ năng giải bài tập

1. Những quy tắc tìm giới hạn vô cực

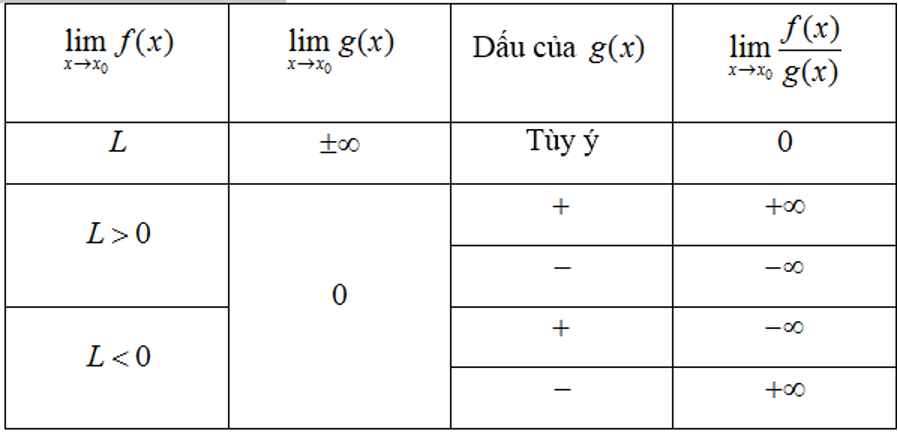
Quy tắc để tìm giới hạn của tích f(x).g(x)

(Dấu của g(x) xét trên một khoảng K nào đó đang được tính giới hạn, với x ≠ x0 )

2. Chú ý:

Các quy tắc trên vẫn đúng với các trường hợp:

Ví dụ 1:

*Lời giải chi tiết

Ta có:

Vì:

Ví dụ 2:

Tìm: 

 Lời giải chi tiết:

Ta có

Vì:

Ví dụ 3:

Tìm 

*Lời giải chi tiết:

Ta có: 

Do đó: 

C. Một số kĩ năng để sử dụng máy tính

1. Giới hạn của hàm số tại một điểm

 –thì ta nhập f(x) và CALC x = a + 10^-9

– thì ta nhập f(x) và CALC x = a – 10^-9

–  thì ta sẽ nhập f(x) và CALC x = a + 10^-9 hoặc x = a – 10^-9

2. Giới hạn của hàm số tại vô cực

–  thì ta sẽ nhập f(x) và CALC x = 10^10.

–  thì ta sẽ nhập f(x) và CALC x = -10^10.

Ví dụ 1: 

Tìm 

Hướng dẫn trả lời:

Ta sẽ nhập biểu thức 

Ấn r máy sẽ hỏi X? Ấn 1+10^p9= máy sẽ hiện 4.

Nên

 

Ví dụ 2:

Tìm  

Hướng dẫn trả lời:

Ta sẽ nhập biểu thức 

Ấn r máy sẽ hỏi X? Ấn 1+10^p9= máy sẽ hiện -999999998.

Nên

 

Ví dụ 3:

Tìm 

Hướng dẫn trả lời:

Ta sẽ nhập biểu thức 

Ấn r máy sẽ hỏi X? Ấn 1p10^p9= máy sẽ hiện 999999998.

Nên

 

Ví dụ 4:

Tìm 

Hướng dẫn trả lời:

Ta sẽ nhập biểu thức  

Ấn r máy sẽ hỏi X? Ấn 10^10= máy sẽ hiện 2.

Nên 

Ví dụ 5:

Tìm 

Hướng dẫn trả lời:

Ta sẽ nhập biểu thức 

Ấn r máy sẽ hỏi X? Ấn 10^10 = máy sẽ hiện 3.

Nên 

 

D: Trả lời câu hỏi và bài tập trong SGK

Hướng dẫn trả lời câu hỏi 1 trang 27 SGK Giải tích 12

Đề bài:

 

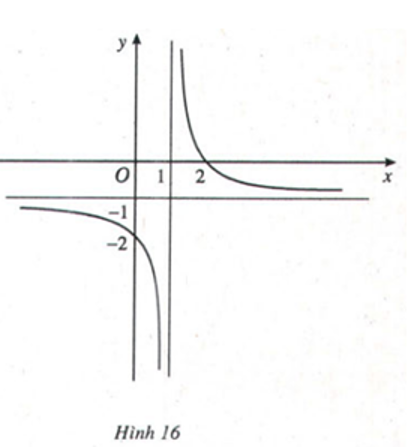
Nêu những nhận xét về khoảng cách từ điểm M(x;y)∈(C) tới đường thẳng y=−1 khi |x|→+∞

Lời giải chi tiết

Khoảng cách từ điểm M(x;y)∈(C) tới đường thẳng y=−1 khi |x|→+∞ dần tiến về 0.

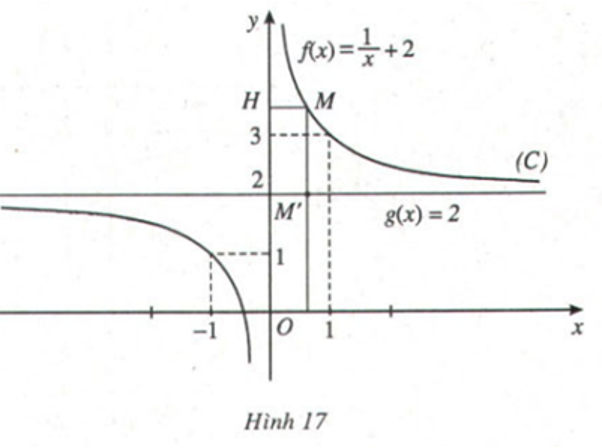
Hướng dẫn trả lời câu hỏi 2 trang 29 SGK Giải tích 12

Đề bài:

Lời giải chi tiết

Khi x tiến dần đến 0 thì độ dài của đoạn MH sẽ dần tiến đến 0.

Trả lời bài 1 trang 30 SGK Giải tích 12

Tìm các tiệm cận của đồ thị hàm số dưới đây:

a) 

*Phương pháp làm bài:

 

nếu như ít nhất một trong các điều kiện dưới đây được thỏa mãn:

Ta kết luận: Đường thẳng x=x0 chính là đường tiệm cận đứng của đồ thị hàm số y=f(x)

*Lời giải chi tiết:

b) 

Lời giải chi tiết:

c)

Lời giải chi tiết:

d)

Lời giải chi tiết:

Do đó đường thẳng y=−1 chính là tiệm cận ngang của đồ thị hàm số.

Trả lời bài 2 trang 30 SGK Giải tích 12

Tìm các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số dưới đây:

a)

Phương pháp làm bài:

– Tìm tiệm cận ngang của đồ thị hàm số: 

– Tìm tiệm cận đứng của đồ thị hàm số:

+ Tìm tập xác định của hàm số

Ta kết luận rằng: Đường thẳng x=x0 chính là đường tiệm cận đứng của đồ thị hàm số y=f(x)

Lời giải chi tiết:

Tập xác định của hàm số: D=R∖{±3} }

b)

Lời giải chi tiết:

c)

Lời giải chi tiết:

Tập xác định của hàm số: D=R∖{−1}

d)

Lời giải chi tiết:

⇒D=[0;+∞)∖{1}

Chú ý: Có thể sử dụng MTCT để tính toán các giới hạn.