Đề cương ôn thi học kì 1 môn Toán 10 là bài viết do HOCMAI sưu tầm, tổng hợp và hệ thống lại kiến thức Toán học kì 1 lớp 10 để gửi tới các em học sinh. Các em sẽ cùng HOCMAI tổng ôn lại tất cả những kiến thức trọng tâm, một số dạng bài thường gặp và luyện tập bằng các đề ôn thi học kì 1 lớp 10 môn toán dưới đây nhé!

⇒ Tham khảo thêm:

• Đề cương ôn thi học kì 1 lớp 10 môn Lý
• Đề cương ôn thi học kì 1 lớp 10 môn Hóa
• Đề cương ôn thi học kì 1 lớp 10 môn Sinh
• Đề cương ôn thi học kì 1 lớp 10 môn Tiếng Anh

I – Đề cương ôn thi học kì 1 môn Toán 10

Phần 1: Mệnh đề – Tập hợp

1. Mệnh đề

– Định nghĩa: Mệnh đề là một câu khẳng định về một sự kiện ở trong toán học. Mỗi mệnh đề toán học phải đúng hoặc sai. Chú ý: Những câu nghi vấn hoặc cảm thán thường không phải là mệnh đề bởi một mệnh đề không thể vừa đúng vừa sai.

– Mệnh đề phủ định: Cho mệnh đề U. Mệnh đề: “không phải U” gọi là mệnh đề phủ định của mệnh đề và kí hiệu là Ū. Nếu U đúng thì Ū sai và ngược lại.

– Mệnh đề kéo theo: 

→ Cho mệnh đề U và I. Mệnh đề: “Nếu U thì I” gọi là mệnh đề kéo theo và kí hiệu là U ⇒ I. Mệnh đề U ⇒ I chỉ sai khi U đúng I sai.

→ Các định lý toán học là những mệnh đề đúng và thường có dạng U ⇒ I. Khi đó ta nói U là giả thiết, I là kết luận của định lý hoặc U là điều kiện đủ để có I hoặc I là điều kiện cần để có U.

– Mệnh đề đảo: Mệnh đề I ⇒ U được gọi là mệnh đề đảo của mệnh đề U ⇒ I.

– Mệnh đề tương đương: Nếu U ⇒ I và I ⇒ U đều đúng thì U và I là hai mệnh đề tương đương. Kí hiệu U ⇒ I và được phát biểu như sau: P tương đương với I; khi P và chỉ khi I; P là điều kiện cần và đủ để I có hoặc nếu P và chỉ nếu I.

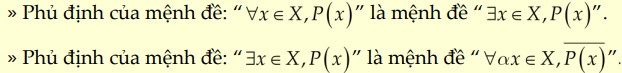
– Các dạng toán thường gặp:

Dạng 1: Bài toán định giá trị của mệnh đề:

– Kiểm tra tính đúng sai của mệnh đề đó

– Nếu mệnh đề chứa biến ⇒ Tìm tập hợp D của các biến x để chứng minh p(x) đúng hoặc sai. 

Dạng 2: Phát biểu định lý dưới dạng bài tập:

– Nếu A ⇒ B đúng thì A là ĐK đủ để có B

– Nếu A ⇒ B sai thì B là ĐK đủ để có A 

– Nếu A ⇒ B đúng và B => A đúng thì A là ĐK cần và đủ để có B 

Dạng 3: Dạng bài tìm mệnh đề phủ định

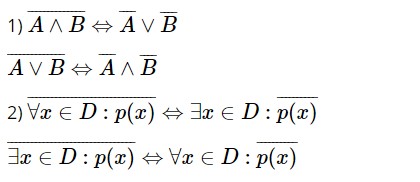
Dạng 4: Chứng minh định lý A ⇒ B 

– Cách 1: Chứng minh A đúng để ⇒ B đúng

– Cách 2: Chứng minh bằng phản chứng: B sai ⇒ A sai 

2. Tập hợp

– Khái niệm tập hợp bao gồm phần tử có chung một hoặc một vài tính chất nào đó. Vd: “Tập hợp các số tự nhiên chia hết cho 4 và nhỏ hơn 40”

– Tập hợp rỗng: Ø

– Tập hợp con: A ⊂ B

– Nếu A ⊂ B và B ⊂ A ⇒ A và B là hai tập hợp bằng nhau. Kí hiệu: A = B

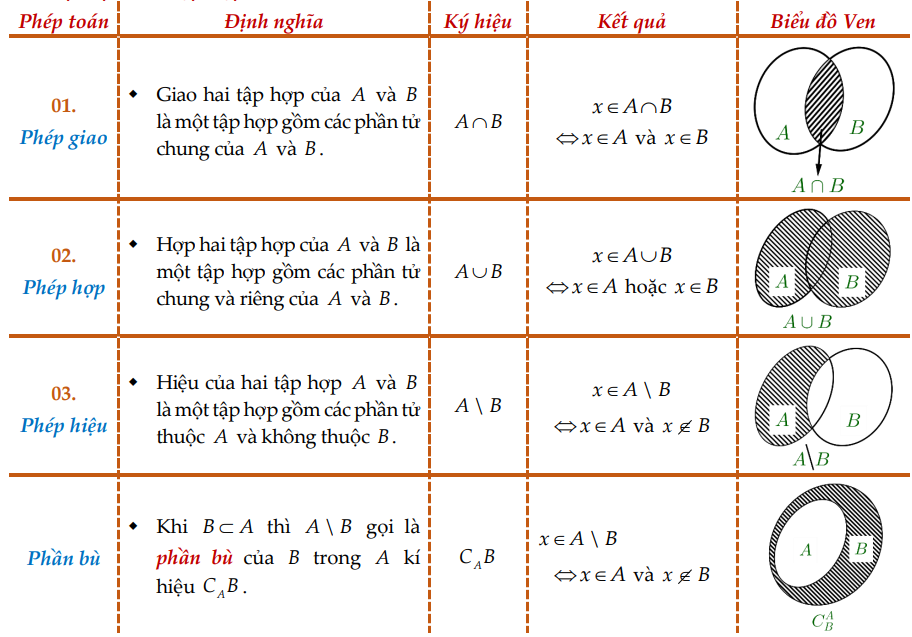
– Các phép toán tập hợp:

– Các tập hợp số:

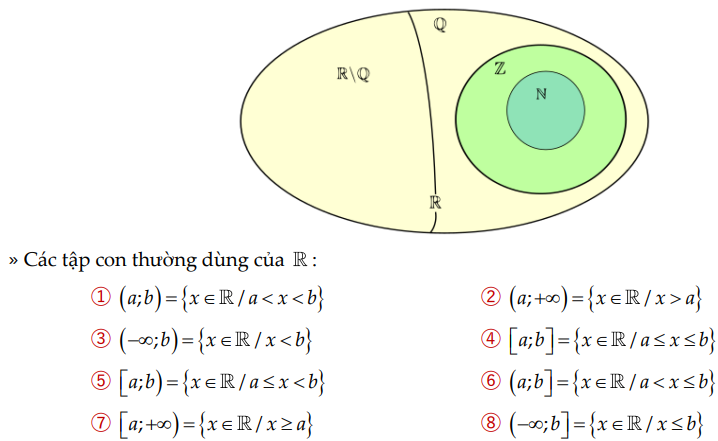
– Các dạng bài về tập hợp:

Dạng 1: Dạng bài tìm tập hợp

– Sử dụng phương pháp liệt kê: A = (a1, a2, a3)

– Nêu tính đặc trưng: A = {x ∈ X | p(x)}

Dạng 2: Dạng bài tìm tập hợp con:

 

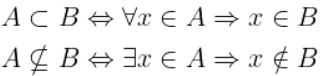
Dạng 3: Dạng bài hai tập hợp bằng nhau:

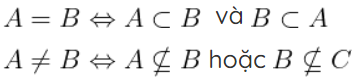
Dạng 4: Dạng bài các phép toán giao, hợp, hiệu

Liệt kê A và B 

• A∩B: Lấy phần tử chung
• A∪B: Lấy phần tử chung và riêng
• A\B: Lấy phần tử của A không phải của B 

Phần 2: Hàm số bậc nhất và bậc hai

1. Tập xác định của Hàm số

Tập xác định của hàm số y=f(x) là tập hợp các số thực x sao cho biểu thức f(x) có nghĩa.

Điều kiện xác định:

• 1/A có nghĩa khi và chỉ khi A ≠ 0
• √A có nghĩa khi và chỉ khi A ≥ 0
• 1/√A có nghĩa khi và chỉ khi A > 0

2. Tính chẵn lẻ của hàm số

Cho hàm số y = f(x) xác định trên D

3. Sự biến thiên

Hàm số y = f(x) xác định trên D

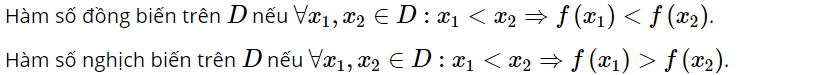
4. Tịnh tiến đồ thị hàm số

Trong Oxy, cho đồ thị (G) của hàm số y = f(x); p và q là hai số dương tùy ý, khi đó:

5. Hàm số bậc nhất

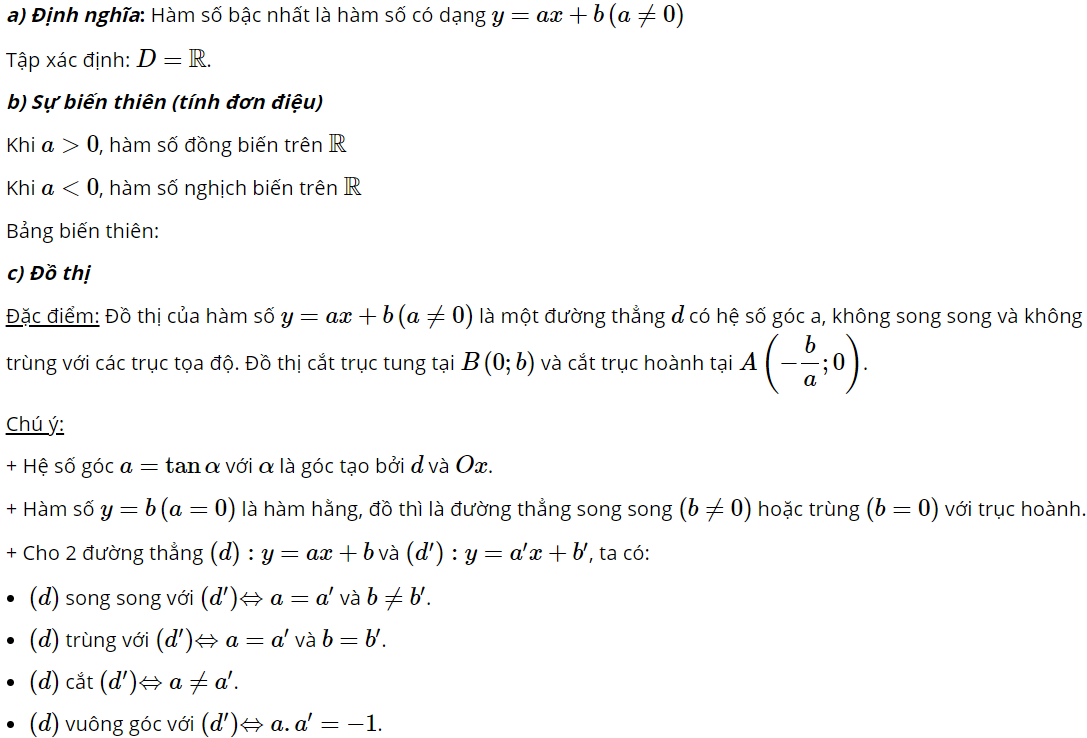
d) Hàm số bậc nhất trên từng khoảng

Hàm số bậc nhất trên từng khoảng là sự “lắp ghép” của những hàm số bậc nhất khác nhau trên từng khoảng. Hàm số có dạng:

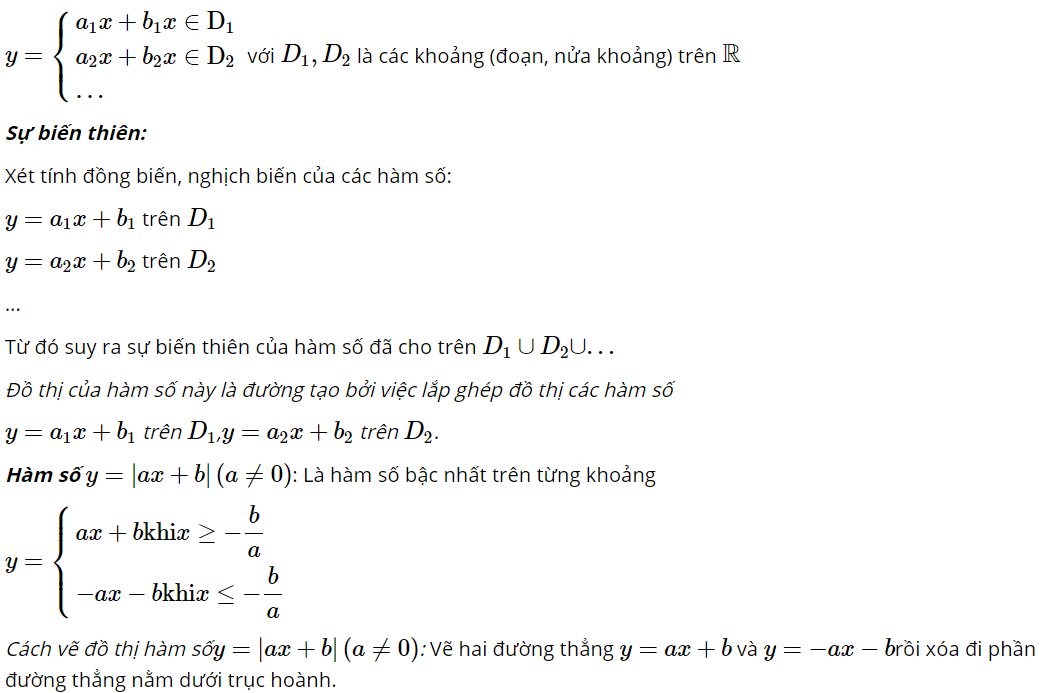
6. Hàm số bậc hai

a) Định nghĩa

Hàm số bậc hai là hàm số có dạng: ax² + bx + c (a≠0)

b) Sự biến thiên

Các dạng toán thường gặp:

Dạng 1: Tìm tập xác định của hàm số

Dạng 2: Xét tính chẵn, lẻ của hàm số

Dạng 3: Xét tính đơn điệu của hàm số

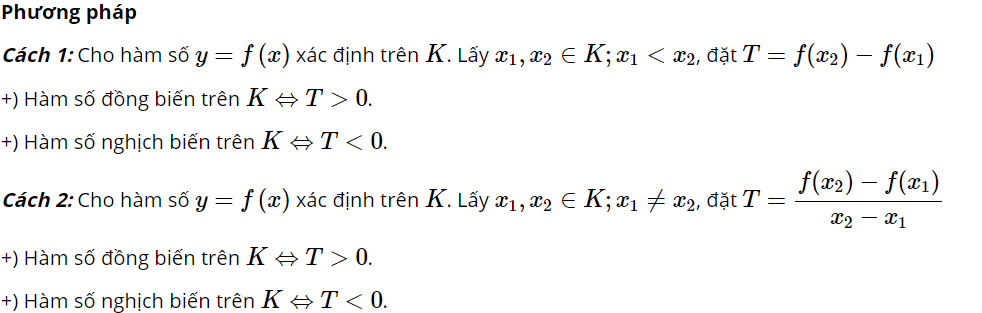
Dạng 4: Đồ thị của hàm số và tịnh tiến đồ thị hàm số

Phương pháp:

Sử dụng định nghĩa điểm thuộc đồ thị hàm số và định lý về tịnh tiến đồ thị một hàm số.

Dạng 5: Xác định hàm số bậc hai

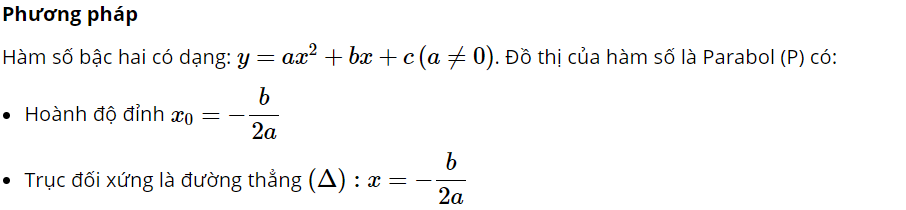
Dạng 6: Tìm GTLN/GTNN nhờ Parabol

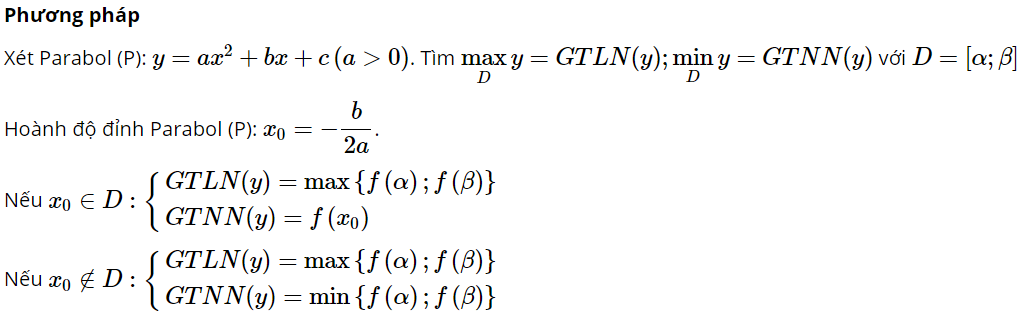
Phần 3: Phương trình – Hệ phương trình

1. Phương trình

a) Định nghĩa

b) Phương trình tương đương và phương trình hệ quả

c) Biến đổi tương đương

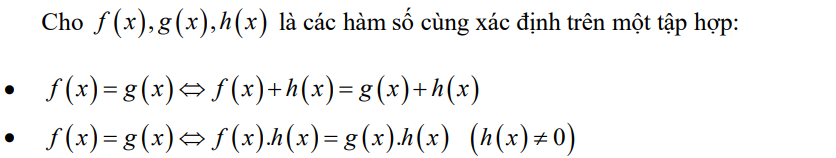
d) Biến đổi hệ quả

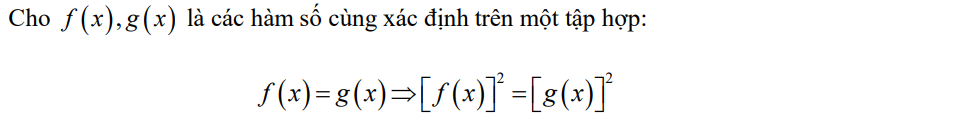
2. Phương trình bậc nhất và phương trình bậc hai một ẩn 

a) Giải và biện luận phương trình dạng ax + b = 0

b) Giải và biện luận phương trình dạng ax² + bx + c = 0

c) Định lý Vi-ét

Hai số x1, x2 là hai nghiệm của phương trình bậc hai ax² + bx + c = 0 khi và chỉ khi:

e) Phương trình chứa ẩn dưới dấu căn bậc hai

Phương trình này thường có thể giải bằng cách bình phương hai vế để khử dấu căn và đưa tới một phương trình hệ quả.

f) Phương trình chứa ẩn ở mẫu thức

Khi giải phương trình này phải để ý đến điều kiện xác định của phương trình

3. Hệ phương trình

a) Giải và biện luận hệ phương trình bậc nhất hai ẩn 

b) Giải hệ phương trình bậc hai hai ẩn

• Hệ phương trình trong đó có một phương trình bậc nhất: Dùng phương pháp thế.
• Hệ phương trình mà mỗi phương trình trong hệ không thay đổi khi thay thế đồng thời x bởi y và y bởi x: Dùng phương pháp đặt ẩn phụ

S = x+y ; P = xy

Các dạng toán thường gặp:

• Dạng 1. Tìm điều kiện xác định của phương trình
• Dạng 2. Giải phương trình 
• Dạng 3. Giải hệ phương trình  
• Dạng 4. Xác định điều kiện của tham số để PT – HPT thỏa mãn điều kiện cho trước

Phần 4: Vectơ

1. Tổng, hiệu của 2 Vectơ

Các quy tắc:

2. Tích của Vectơ với một số

3. Hệ trục tọa độ

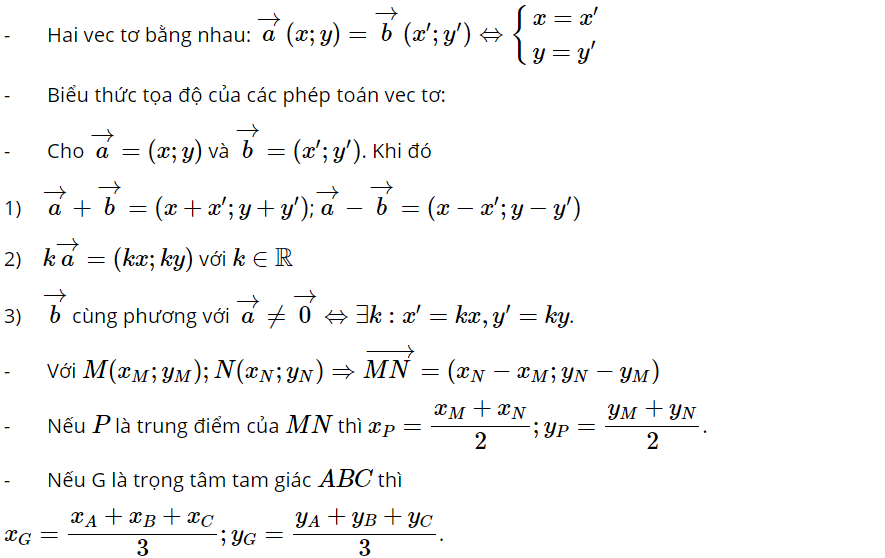
Phần 5: Tích vô hướng của hai vectơ và ứng dụng

1. Tích vô hướng của hai vectơ

a) Định nghĩa

2. Hệ thức lượng trong tam giác

a) Giá trị lượng giác của góc từ 0° đến 180°:

• Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O nằm phía trên trục hoành bán kính R = 1 được gọi là nửa đường tròn đơn vị.
• Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định một điểm M trên nửa đường tròn đơn vị sao cho xOM = α và giả sử điểm M có tọa độ M(xo;yo). Khi đó ta có định nghĩa:

b) Hệ thức lượng trong tam giác:

• Định lý Côsin:

• Định lý Sin:

Các dạng toán thường gặp:

• Dạng 1. Tính tích vô hướng của vectơ và các thông số liên quan
• Dạng 2. Biểu thức tọa độ liên quan đến tích vô hướng của hai vectơ
• Dạng 3. Tìm điểm thỏa mãn điều kiện cho trước
• Dạng 4. Giải tam giác
• Dạng 5. Bài toán cực trị

→ Tham khảo chi tiết Đề cương ôn thi học kì 1 môn toán lớp 10 ngay tại đây (↓):
 

II – Tham khảo một số đề ôn thi học kì 1 môn Toán 10 theo chương trình mới 

Đề ôn thi học kì 1 lớp 10 môn toán – Đề số 1 

⇒ Xem chi tiết đáp án TẠI ĐÂY!

Đề ôn thi học kì 1 lớp 10 môn toán – Đề số 2 

⇒ Xem chi tiết đáp án TẠI ĐÂY!

Đề ôn thi học kì 1 lớp 10 môn toán – Đề số 3 

⇒ Xem chi tiết đáp án TẠI ĐÂY!

Bộ đề thi học kì 1 Toán 10 Kết nối tri thức với cuộc sống

Bộ đề ôn thi học kỳ 1 Toán lớp 10 Kết nối tri thức với cuộc sống gồm 5 đề trắc nghiệm + đáp án chi tiết. Tham khảo tại đây:

Bộ đề thi học kì 1 Toán 10 Cánh diều

Bộ đề ôn thi học kỳ 1 Toán lớp 10 Kết nối tri thức với cuộc sống gồm 4 đề trắc nghiệm + đáp án chi tiết. Tham khảo tại đây:

Bộ đề thi học kì 1 Toán 10 Chân trời sáng tạo

Bộ đề ôn thi học kỳ 1 Toán lớp 10 Kết nối tri thức với cuộc sống gồm 2 đề trắc nghiệm + đáp án chi tiết. Tham khảo tại đây:

Trên đây là bài viết Đề cương ôn thi học kì 1 môn Toán 10. Bài viết này HOCMAI đã tổng hợp rất đầy đủ kiến thức, bài tập và đề luyện để các em có thể an tâm đi thi. Chỉ cần học thuộc lòng lý thuyết và làm thêm nhiều đề hơn nữa thì bài thi cuối học kì 1 sẽ trở nên thật dễ dàng. Nếu như có bất kỳ khó khăn hay thắc mắc nào trong quá trình ôn luyện thi, các em hãy chủ động hỏi thầy cô và bạn bè nhé!