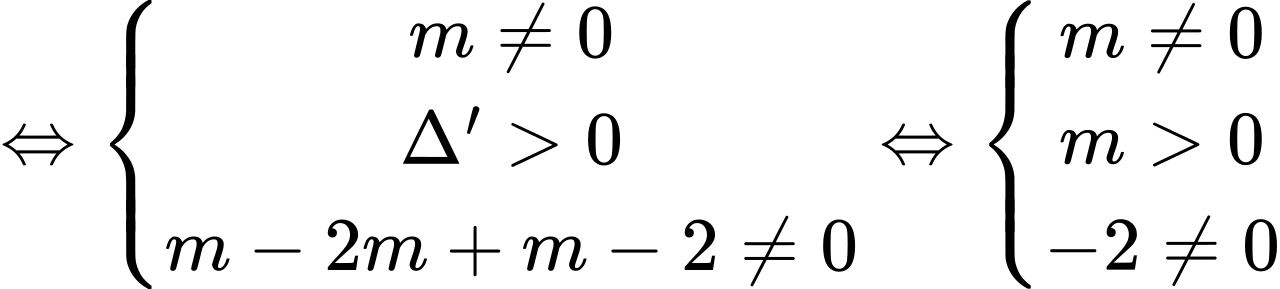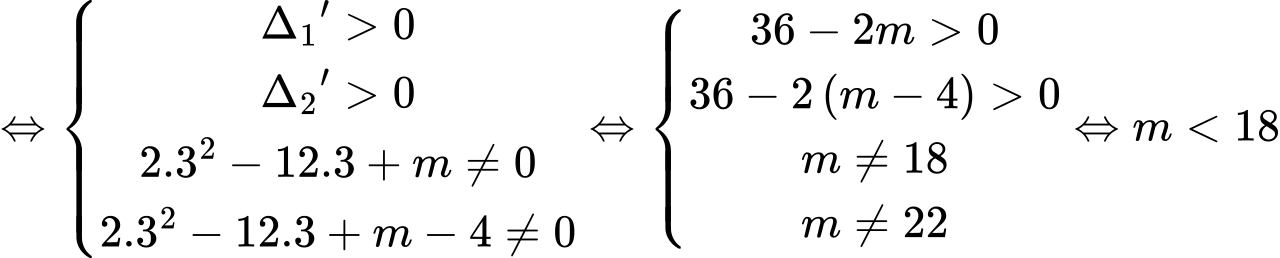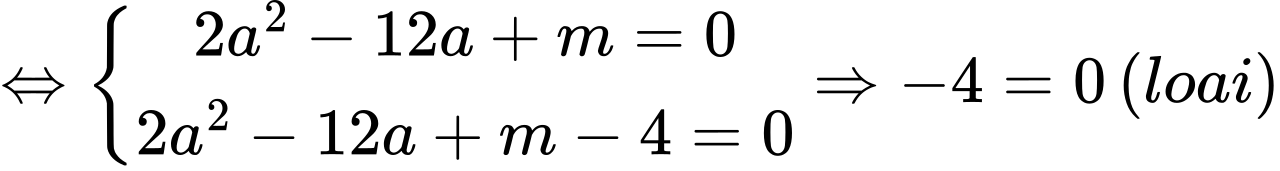Để giúp cho các bạn học sinh lớp 12 học tập tốt hơn với môn Toán, butbi sẽ hướng dẫn các bạn làm dạng bài tìm m để hàm số có 5 cực trị. Bài viết sẽ giới thiệu đến bạn đọc những phương pháp giải dạng bài tập ứng dụng tìm tham số m để hàm số đã cho có cực trị cùng với hướng dẫn giải chi tiết, được xây dựng dựa trên khối kiến thức trọng tâm chương trình Toán lớp 12 và các câu hỏi đã trong đề thi THPT Quốc gia các năm. Hi vọng bài viết này sẽ giúp cho các bạn ôn thi luyện kiến thức thi học kì, thi tốt nghiệp THPT Quốc gia 2023 môn Toán trắc nghiệm đạt hiệu quả.

Tham khảo thêm:

• Cực trị của hàm số
• Tìm m để hàm số có 7 cực trị
• Tìm m để hàm số có 3 cực trị
• Tìm m để hàm số có 2 cực trị
• Tìm m để hàm số có đúng 1 cực trị

Bài tập tìm m để hàm số có 5 cực trị có đáp án

Tìm m để hàm số có 5 cực trị (ví dụ 1)

Cho đồ thị hàm số y = f’(x) giống như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = f(|x| + m) sẽ có 5 điểm cực trị?

 

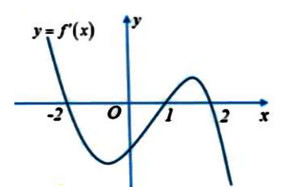
Bài giải chi tiết:

Hàm số y = f(|x| + m) chính là hàm số chẵn

Với x > 0 → y = f(|x| + m) = f(x + m) ⇒ y’ = f’(x + m)

• y’ = f’(x + m) = 0

Hàm số y = f(|x| + m) sẽ có 5 điểm cực trị khi và chỉ khi y = f(|x| + m) có 2 điểm cực trị dương hay:

Vậy sẽ có 3 giá trị nguyên của m để hàm số đã cho: y = f(|x| + m) có 5 điểm cực trị.

Tìm m để hàm số có 5 cực trị (ví dụ 2)

Có bao nhiêu giá trị nguyên của m ∈ [-10; 10], để hàm số sau đây: y = |mx³ – 3mx² + (3m – 2)x + 2 – m| sẽ có 5 điểm cực trị?

Bài giải chi tiết:

Ta xét các trường hợp lần lượt như sau:

*Trường hợp 01: Với m = 0

Thay vào hàm số y = |mx³ – 3mx² + (3m – 2)x + 2 – m| ta được y = |-2x + 2| có 1 điểm cực trị vậy m = 0 loại

*Trường hợp 02: Với m ≠ 0

Hàm số y = |mx³ – 3mx² + (3m – 2)x + 2 – m| sẽ có 5 điểm cực trị khi và chỉ khi đồ thị của hàm số f(x) = mx³ – 3mx² + (3m – 2)x + 2 – m cắt trục hoành ở 3 điểm phân biệt.

Ta xét phương trình:

f(x) = 0 ⇔ mx³ – 3mx² + (3m – 2)x + 2 – m = 0 ⇔ (x – 1)(mx² – 2mx + m – 2) = 0

⇔ 

Để f(x)=0 có được 3 nghiệm phân biệt thì (*) có 2 nghiệm phân biệt khác với nghiệm x = 1

 

Do trong đề bài m ∈ [-10; 10] ⇒ m ∈ (0; 10]

♦ Vậy sẽ có 10 giá trị của m thỏa mãn yêu cầu.

Tìm m để hàm số có 5 cực trị (ví dụ 3)

Cho hàm số f(x) và có đạo hàm f’(x) = (x + 1)²(x² – 4x). Có tổng bao nhiêu giá trị nguyên dương của m để hàm số g(x) = f(2x² – 12x + m) sẽ có đúng 5 điểm cực trị?

Hướng dẫn giải chi tiết

Với g'(x) ta có:

g’(x) = (4x – 12) . f’(2x² – 12x + m) = (4x – 12) . (2x² – 12x + m + 1)² . (2x² – 12x + m) . (2x² – 12x + m – 4)

Hàm số g(x) đã có đúng 5 điểm cực trị khi:

→ g’(x) sẽ đổi dấu 5 lần

→ g’(x) = 0 sẽ có 5 nghiệm đơn phân biệt

→ Phương trình 2x² – 12x + m = 0 sẽ có 2 nghiệm phân biệt khác 3 và phương trình 2x² – 12x + m – 4 = 0 cũng sẽ có 2 nghiệm phân biệt khác 3 và các nghiệm này đều khác nhau

*Phương trình 2x² – 12x + m = 0 có 2 nghiệm phân biệt khác 3 và phương trình 2x² – 12x + m – 4 = 0 có 2 nghiệm phân biệt khác 3

 

Vậy với điều kiện tham số m < 18 giả sử 2 phương trình đều có nghiệm chung là a

Thay x = a vào hai phương trình đã cho chúng ta được

 

Do đó các nghiệm của 2 phương trình 2x² – 12x + m = 0 và pt 2x² – 12x + m – 4 = 0 luôn khác nhau.

Mà m chính là số nguyên dương nên m ∈ {1; 2; 3; ….; 17}

Như vậy Có 17 giá trị của m thỏa mãn các điều kiện của đề bài.